Prim's Algorithm

Minimum Spanning Tree

Greedy 알고리즘의 예시인 Prim's Algorithm을 살펴보기 전에

그 알고리즘이 다루는 Minimum Spanning Tree의 정의부터 알아보자.

 

- Tree

Graph 구조에서 cycle 구조가 존재하지 않고, 연결되지 않은 vertex가 없고, edge에 방향성이 없는 그래프.

 

- Spanning Tree

오리지널 Tree의 부분 트리. 즉, 오리지널 Tree에서 일부 edge가 없는 트리를 의미한다.

 

- Minimum Spanning Tree

Spanning Tree 중, edge의 weight의 합이 최소가 되는 트리.

G1이 오리지널 트리라 했을 때, G4, G5만이 G1의 Minimum Spanning Tree이다.

G2의 경우에는 G1에 Spanning하긴 하지만, Tree가 아니고,

G3의 경우에는 G1의 Spanning Tree이긴 하지만, Minimum하지 않다.

 

Prim's Algorithm

이 알고리즘은 그리디 기법을 이용해서 Graph에서 Minimum Spanning Tree를 찾는 알고리즘이다.

위 방식대로 진행된다면 Y집합에는 vertex가, F집합에는 node가 들어가게 되는데,

집합에 추가하는 방식은 다음과 같다.

 

1. V1를 Y에 추가한다.
2. Y와 연결된 vertex 사이의 edge를 찾는다. (연두색 하이라이트)
3. 찾은 edge 중, weight가 가장 작은 edge에 연결된 vertex를 Y에 추가한다.
4. Y에 모든 vertex가 들어갈 때 까지 반복한다.

 

위 알고리즘을 의사코드로 구현해보자.

구현하기에 앞서 몇 가지 규칙을 정하자.

W[i][j]: Vi - Vj를 연결하는 edge의 weight. (즉, W는 weight table이고, symmetric하다)
nearest[i]: Y에 들어있는 vertex 중, Vi와의 거리가 가장 가까운 vertex의 index.
distance[i]: Vi와 nearest[i]로 인덱싱된 Y에 들어있는 vertex 사이의 거리.

 

위 규칙에 따르면 초기화는 다음과 같이 진행되어야 한다.

• nearest[i]는 1로 초기화 한다.
  처음에는 Y에 V1만 들어있기 때문.
• distance[i]는 W[1][i]로 초기화 한다.
  처음에는 모든 nearest[i]로 인덱싱된 vertex가 V1이기 때문.

 

이제 의사코드를 살펴보자.

public static setOfEdge prim(int n, const number W[][]) {
    index vnear; // weight가 최소가 되는 vertex의 index를 저장할 변수
    index[] nearest = new index[2..n];
    number min; // weight의 최솟값을 저장할 변수
    number[] distance = new number[2..n];
    setOfEdge F = {};

    for (index i=2; i<=n; i++) {
        nearest[i] = 1;
        distance[i] = W[1][i];
    }

    repeat(n-1 times) {
        min = INF;
        for (index i=2; i<=n; i++) {
            // 0보다 큰지 비교하는 이유:
            // 아래 코드에서 e를 추가할 때 distance[vnear] = -1로 변경해주는데,
            // distance가 -1일 때의 Vi는 이미 Y집합에 포함됨을 표시하기 위함이다.
            if (0 <= distance[i] < min) {
                min = distance[i];
                vnear = i;
            }
        }

        Edge e = vnear로 인덱싱된 vertex와 nearest[vnear]로 인덱싱된 vertex를 잇는 edge;
        add e to F;
        distance[vnear] = -1; // add Vvnear to Y

        for (index i=2; i<=n; i++) {
            if (W[i][vnear] < distance[i]) {
                distance[i] = W[i][vnear];
                nearest[i] = vnear;
            }
        }
    }

    return F;
}

이 때의 각 변수를 추적해보면 아래와 같은 상태일 것이다.

• nearest[2..5] = [1, 1, 2, 1] (이전 스탭에는 [1, 1, 1, 1]이었을 것)
• distance[2..5] = [-1, 3, 6, INF] (이전 스탭에는 [1, 3, INF, INF] 이었을 것)
• F = {(V1, V2)} (이전 스탭에는 {} 이었을 것)

 

 

참고로 위 알고리즘의 시간 복잡도는 if (W[i][vnear] < distance[i]) { 를 basic op로 할 때, Θ(n^2) 이다.

 

Optimality

그렇다면, 과연 그리디 기법으로 만든 Prim 알고리즘은 최적해를 도출해주는 것일까?

그리디 기법은 순간순간의 최고의 선택을 이어 결과를 도출하는데,

이는 명백히 Dynamic Programming 기법과는 달라 최적해를 도출해주는지에 대한 검증이 필요하다.

 

이를 검증하기 위해 promising 이라는 개념을 도입하자.

promising이란, 미래에 원하는 결과를 도출할 수 있는 가능성이 있는 상태를 의미한다.

 

Prim 알고리즘에서는 아래의 상황을 promising 하다고 표현한다.

G의 부분집합 F에 0개 이상의 edge를 추가했을 때,
minimum spanning tree가 된다면, F는 promising하다.

 

예시를 들어보자.

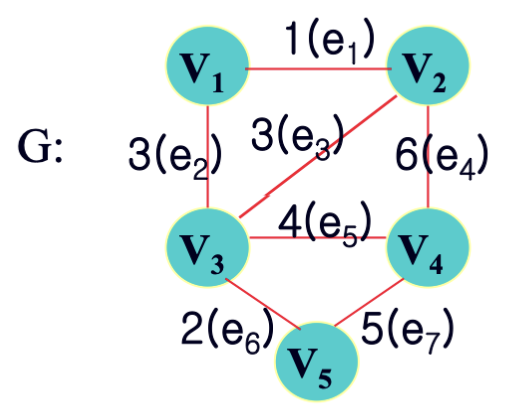
1. F = {}
2. F = {e4}
3. F = {e1, e2}
4. F = {e1, e2, e3}
5. F = {e1, e2, e5}
6. F = {e1, e2, e5, e6}

 

위 경우서는 2, 4를 제외하고 promising 하다.

그 이유는 1, 3, 5, 6의 경우에는 특정 edge를 추가할 경우 minimum spannig tree를 만들 수 있지만,

2, 4의 경우에는 어떠한 edge를 추가해도 minimum spanning tree를 만들 수 없기 때문이다.

 

이런 promising를 점화식 형태로 사용하면 Prim 알고리즘이 최적해를 도출한다는 사실을 증명할 수 있다.

 

1. F = {}는 promising 하다. (자명)
2. 몇 번의 과정을 거친 F가 promising 하다고 가정한다.
3. 다음 루프의 F (즉 F union {e})가 promising 한 것을 증명한다.
   (여기서 e는 Y와 나머지 vertices를 잇은 edge 중 최소 weight를 갖는 edge)

 

여기서 위 점화식이 참이라면 아래와 같은 관계가 성립된다.

F는 promising하기 때문에, F를 부분집합으로 갖고있는 F'가 존재할 것이고,
F'역시 promising, 즉 minimum spanning tree이다.

 

이 때 두 가지 경우로 나뉘게 되는데, F가 F'로 되기 위한 과정에서 특정 edge e를 추가할 때,

e가 F'에 포함된 edge인지, 포함되지 않는 edge인지로 나뉘게 된다.

각각의 경우 모두 F union {e}가 promising 한 것을 증명해야 한다.

 

- Case 1: F'가 e를 포함하는 경우

이 경우에는 F union {e}가 F'의 부분집합 이므로 promising 하다는 것이 자명하다.

 

- Case 2: F'가 e를 포함하지 않는 경우

이 경우에는 F union {e}는 F'의 부분집합이 아니다.

하지만, F' union {e} - {e'}의 부분집합이긴 하다.

이 때, F' union {e} - {e'} 역시 점화식의 가정에 의해 promising, minimum spanning tree여야 한다.

 

그렇기에 e'의 크기는 e보다 작거나 같아야 하는데, 

작은 경우에는 F'가 minimum하지 않는다는 뜻이 되기에 사실 e와 e'의 weight는 같아야 한다.

(즉, F' 단계에서는 minimum spanning tree를 달성하기 위한 경로가 2개 이상 존재한다는 뜻)

 

결국 F'나 F' union {e} - {e'} 모두 promising, minimum spanning tree이고,

F union {e}는 F' union {e} - {e'}의 부분집합이기 때문에

F union {e}는 promising하다.