Huffman Code

Huffman Code는 데이터를 압축하는데 있어 효과적인 인코딩 방법으로,

텍스트 파일을 가변길이의 이진코드로 변환하는데 사용된다.

 

예로 들어 허프만 코드로 a: 10, b: 0, c: 11로 변환한다면

ababcbbbc는 1001001100011로 변환된다.

ababcbbbc는 9bytes 즉, 72bit를 사용해서 저장해야 하지만,

허프만 체계로 변환된 1001001100011은 13bit면 저장이 가능하다. (복호화에 필요한 헤더 제외)

 

a: 10, b: 0, c: 11와 같은 코드로 변환할 때는 prefix code로 변환해야만 한다.

prefix code란, 어떤 문자를 나타내는 코드는

다른 문자를 나타내는 코드의 앞 부분과 반드시 다른 코드체계를 의미한다.

 

prefix code로 구성해야지만 0이 들어오면 바로 b로 확정지을 수 있고,

1이 들어오는 경우는 b를 탐색 범위에서 제외하고 다음 비트로 결정하도록 구현할 수 있다.

이런 탐색 과정은 이진트리를 이용하면 구현할 수 있다.

즉, leaf node에 도달하는 과정에 있는 비트를 이어붙이면 leaf node에 있는 문자의 허프만 코드가 된다.

 

그렇다면, 허프만 코드를 효율적으로 구성하려면 이 노드를 어떻게 구성해야 할까?

depth가 낮다는 것은 허프만 코드가 짧다는 것을 의미한다.

따라서 빈도가 가장 높은 문자의 허프만 코드를 짧게 되도록 배치하면,

전체 문자열을 허프만 코드로 변환했을 때 인코딩 된 전체 비트수도 짧아질 것이다.

 

그 배치하는 과정을 Greedy한 방식으로 구현하게 된다.

 

Huffman's Algorithm

이 알고리즘의 동작 과정을 살펴보자.

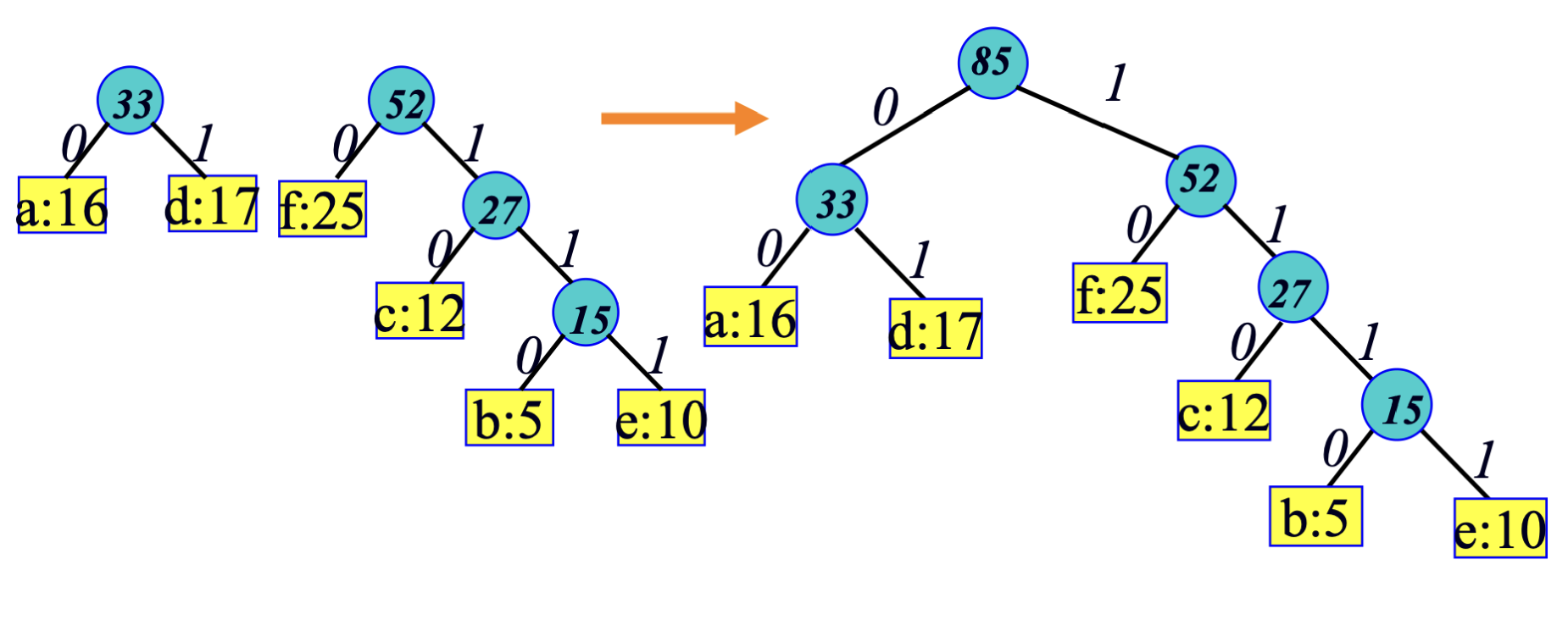
각 노드는 문자:빈도수의 정보를 담고있는데,

가장 빈도수가 낮은 두 노드를 뽑아 트리를 구성하고 트리의 root의 값은 두 빈도수의 합으로 한다.

빈도수(의 합)이 낮은 노드를 계속해서 뽑아 하나의 트리로 합쳐질 때 까지 반복하게 된다.

 

빈도수가 낮은 노드를 우선적으로 트리를 구성함으로써 depth를 먼저 깊게 만드는 효과가 있다.

즉, 빈도수가 높은 노드(문자)는 depth가 낮아지게 된다.

이 때, 빈도수가 낮은 두 노드를 뽑는 과정은 우선순위 큐를 이용하면 쉽게 구현할 수 있다.

 

위 알고리즘을 의사코드로 구현해보자.

public class nodeType {
    char symbol;
    int frequency;
    
    nodeType left;
    nodeType right;
}

PQ = 우선순위 큐 (min priority queue);
public static nodeType huffman() {
    nodeType p, q, r;
    
    for (i=0; i<n; i++) {
        remove(PQ, p);
        remove(PQ, q);
        
        r = new nodeType();
        r.left = p;
        r.right = q;
        r.frequency = p.frequency + q.frequency;
        
        isnert(PQ, r);
    }
    remove(PQ, r);
    
    return r
}

위 알고리즘의 시잔 복잡도는 Θ(n lg n)을 갖는다.

 

Optimality

그리디 기법으로 만든 Huffman's Algorithm은 최적해를 도출해줄까?

이를 검증하기 위해 우선 branch라는 개념을 도입하자.

 

branch란, optimal prefix binary tree 이루는 부분트리로 정의하자.
(위 그림에서 노란 삼각형(부분트리)에 해당)

참고로 leaf node 하나로도 branch를 이룰 수 있다.

 

이제 branch를 이용해서 점화식을 이용해서 증명해보자.

 

1. 0번째 스탭에서 leaf node는 optimal prefix binary tree T의 branch가 된다. (자명)
2. i번째 스탭에서 부분트리들은 T의 branch라고 가정.
3. i+1번째 스탭에서 두 부분트리 u, v를 합친 트리가 T의 branch가 됨을 증명.

 

이 때, 트리를 합칠 때에 있어 3가지 유의할 점이 있다.

첫번째로 왼쪽의 서브트리와 오른쪽의 서브트리를 바꿔도 여전히 optimal prefix binary tree가 된다.

(01이 10이 될 뿐의 차이만 존재한다)

 

두번째로 같은 depth를 갖는 서브트리를 swap해도 여전히 optimal prefix binary tree가 된다.

(depth가 같기 때문에 freq*depth의 결과는 같아질 것)

 

마지막으로 같은 frequency를 갖는 서브트리를 swap해도 여전히...(이하생략)

(빈도수가 같기 때문에 freq*depth의 결과는 같아질 것)

 

위 유의점을 고려하여 점화식 3단계를 증명해보자.

 

- Case 1: u, v의 부모가 같을 때

i=3 step에서 u, v를 선택한 꼴이다.

즉 u & v는 branch가 된다.

 

- Case 2: u, v의 부모가 다를 때

이 때는 u의 depth가 v의 depth보다 깊다고 가정하고,

w라는 다른 branch의 부모와 u의 부모가 같다고 가정하자.

이 때 위의 유의점에 의해 w와 v를 swap해도 optimal하다.

즉 부모가 달라도 frequency가 같다면,

u & v는 T'의 branch가 된다.

 

만약 frequency가 다르다면?

다르다 하더라도 w의 frequency는 반드시 v의 frequency보다 크거나 같다.

그 이유는 우선순위 큐를 이용해서 u, v를 뽑았기 때문에,

뽑히지 않는 w의 frequency는 반드시 뽑힌 v보다 크거나 같을 수 밖에 없다.

 

또한, w의 depth는 반드시 v보다 깊거나 같은데,

그 이유는 Case 2의 가정에서 u의 depth가 v보다 깊다고 가정했는데,

w는 u의 sibling이기 때문에 w가 v보다 depth가 더 깊을 수 밖에 없다.

 

따라서 cost(T')와 cost(T)의 관계는 다음과 같아진다.

cost(T') = cost(T)
                  + (depth(w) - depth(v)) * frequency(v)  // v, w swap시 v가 깊어진 만큼의 cost 추가
                  - (depth(w) - depth(v)) * frequency(w)  // v, w swap시 w가 얕아진 만큼의 cost 제외
               <= cost(T)  // w의 frequency가 더 크기 때문에 결과적으로 더 작아짐

 

즉, cost(T') <= cost(T)인데 만약 더 작다면 T가 사실은 optimal하지 않았다는 소리가 되어버린다.

따라서 둘은 같을 수 밖에 없고, 둘이 같아지려면 v와 w의 frequency는 같을 수 밖에 없다.

따라서 애초에 v와 w의 frequency가 다를 일은 없다.