Traveling SalesPerson Problem (Dynamic Programming)

- 알고리즘 정의

주어진 Graph의 모든 노드를 한 번씩 방문하여 출발했던 노드로 돌아오는 방법 중,

가장 최단 시간으로 걸리는 경로를 찾는 문제이다. 

일명 TSP 알고리즘이다.

위 예시에서는 v1 - v3 - v4 - v2 - v1로 방문하면 최단 시간이 걸린다.

참고로 출발점은 임의로 잡아도 상관 없다.

왜냐하면 모든 노드를 한 번씩 방문하기 때문에 반드시 특정 노드를 어느 순간 지나기 때문이다.

다만, 이해와 구현의 편의성을 위해 v1을 시점이자 종점으로 삼자.

 

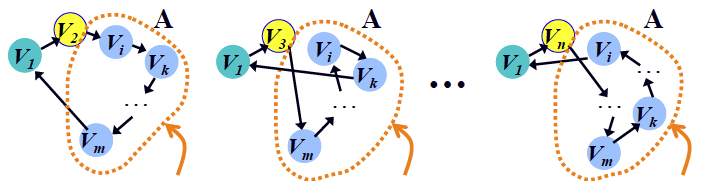
최적의 경로는 위 경로 중 하나의 경우다.

v1 - v2 를 지나 최적 경로 A를 지나 v1로 돌아오거나,

v1 - v3 를 지나 최적 경로 A를 지나 v1로 돌아오거나, ...,

v1 - vn 를 지나 최적 경로 A를 지나 v1로 돌아오거나.

 

위의 방식대로 알고리즘을 설계하기 위해 다음과 같은 규칙을 만들자.

• V: {v1, v2, ..., vn}, 모든 vertices의 집합
• A: V의 부분집합
• W[i][j]: vi -> vj의 length(weight)
• D[vi][A]: vi 에서 A의 모든 vertices를 지나 v1로 돌아오는 최단 경로의 길이
• D[vi][∅]: vi 에서 아무런 vertex를 지나지 않고 v1로 돌아오는 최단 경로의 길이
                  즉, W[i][1]

 

최종적으로 구하고자 하는 값인 D[v1][V-{v1}]은 v1 - vj 순서로 먼저 시작한다고 하면

min(W[1][j] + D[vj][V-{v1, vj}]) (j: 2~n)로 구할 수 있다.

이를 일반화하여 D[vi][A] = min(W[i][j] + D[vj][A-{vj}]) (vj: A의 원소)라는 관계를 얻을 수 있다.

 

위에서 직관적으로 최단경로를 구한 예시를 이번엔 위 수식을 이용해서 구해보자.

Case sizeof A = 0:

 

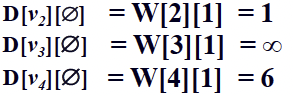
Case sizeof A = 1:

 

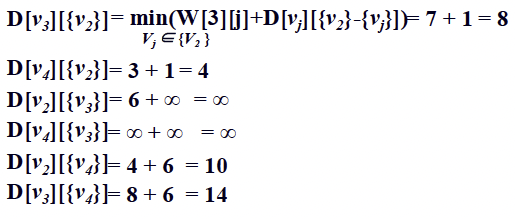
Case sizeof A = 2:

 

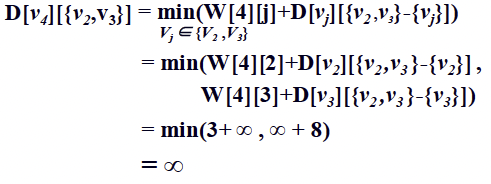
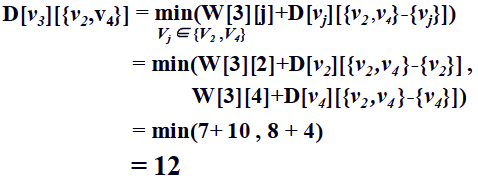
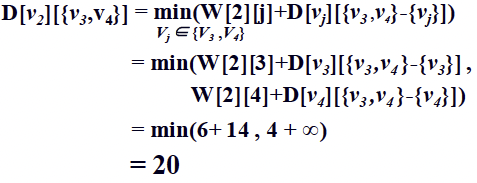
Case sizeof A = 3 (Goal)

 

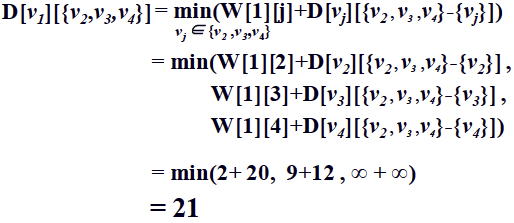
- Pseudocode

// global: V (vertices)
public static number tsp (int n, number[][] W, index[][] P) {
    index i, j, k;
    number[][] D = new number[1..n][subset of V-{v1}];
    
    // 0개의 노드를 통과해 v1로 가는 경로의 최단거리
    for (i=2; i<=n; i++)
        D[i][∅] = W[i][1];
    
    // 1~n-2개의 노드를 통과해 v1로 가는 경로의 최단거리
    for (k=1; k<=n-2; k++)
        // k개의 원소를 가진 모든 V-{v1}의 부분집합 A에 대해
        for (all subsets A of V-{v1} containing k nodes)
            // vi는 v1, A의 원소이면 안 된다.
            for (i such that i!=1 && vi is not in A) {
                // j는 A의 원소 vj의 V에 대한 인덱스 (min은 sizeof A의 loop를 돈다)
                D[i][A] = min(W[i][j] + D[j][A-{vj}]);
                // 최소가 되게 하는 vj의 인덱스
                P[i][A] = j;
            }
    
    // n-1개의 노드를 통과해 v1로 가는 경로의 최단거리
    // (min은 n-2의 loop를 돈다)
    D[1][V-{v1}] = min(W[1][j] + D[j][V-{v1, vj}]);
    P[1][V-{v1}] = j;
    
    return D[1][V-{v1}];
}

알고리즘 설명대로 진행된다.

 

V는 vertices들이 들어있는 전역 배열

n은 V의 노드(vertex)의 갯수

W는 weight(길이) 테이블

P는 최단 경로를 저장할 배열이다.

 

결과적으로 D[vi][A]에는 vi에서 출발해 A의 vertices를 지나 v1로 도달하는데 까지 최단 거리가 저장되고,

P[vi][A]에는 vi에서 출발해 A의 vertices를 지나 v1로 도달하는데 최단 거리가 되기 위해

vi 다음으로 지나야 할 A의 원소인 vertex의 인덱스를 저장하게 된다.

 

- Time complexity

Basic Operation: min 함수 내부의 j(vj) loop 반복 횟수

Input Size: n, number of vertices

 

* Every case:

Within min-loop: sizeof A = k times

Within i-loop: (n - sizeof A - 1(for v1))k = (n-k-1)k times

Within A-loop: (number of subset A)(n-k-1)k = C(n-1, k)(n-k-1)k times

[Θ(n^2*2^n)]