Query Processing

Overview

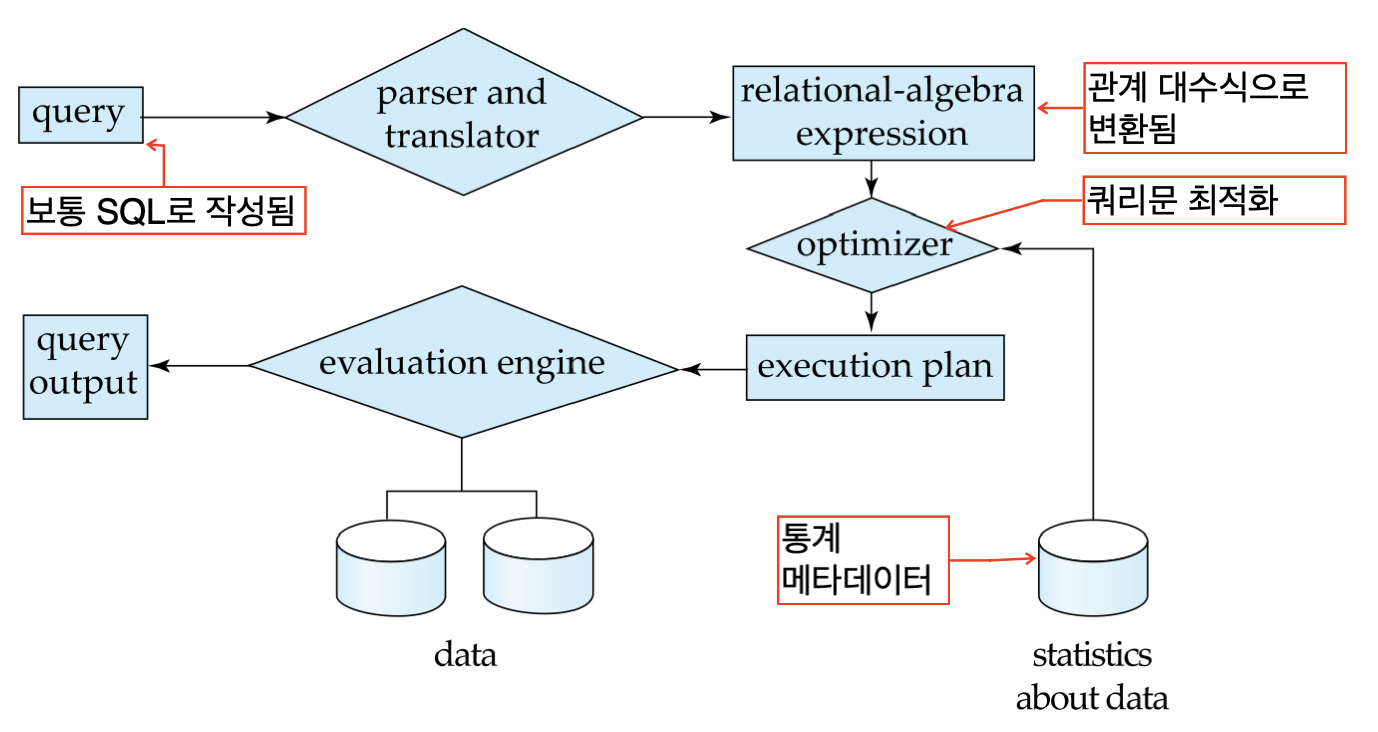
parser and translator에서 문법 검사과 유효한 테이블에 접근하는지 검사한다.

evaluation engine에서 최적화된 실행 계획에 맞게 쿼리문을 실행한다.

optimizer는 같은 결과를 내는 여러 관계 대수식(실행문) 중 Cost가 가장 낮은 실행문을 고른다.

 

Cost

Disk access, CPU, network communication 등의 시간 비용을 의미한다.

여기서는 CPU비용은 너무 작으니 무시하도록 하고,

분산 시스템에서는 network communication이 중요하지만, 여기선 단일 시스템으로 가정하기에 역시 무시한다.

Disk access는 실제 시간이 아닌, 몇 블럭을 읽어오는지, 공간 단위로 측정하도록 한다.

 

Disk cost는 아래와 같은 비용들로 구분할 수 있다.

Number of seeks	디스크 헤더가 탐색하는 시간
Number of read	블럭을 읽어오는 시간
Number of written	블럭을 쓰는 시간

 

계산의 편의성을 위해 읽고 쓰는데 비용은 같다고 가정하고, 버퍼도 사용 안한다고 가정한다.

 

$$ t_T: \; 한; 블럭 \; 전송하는데 \; 걸리는 \; 시간 $$

$$ t_S: \; seek \; 하는데 \; 걸리는 \; 시간 $$

 

Selection Operation

disk 탐색시 seek의 오버헤드가 크기 때문에 이런 경우에는 binary search보다

linear search의 효율이 더 좋을 수 있다.

따라서 linear search 방식으로 탐색하며 조건에 맞는 데이터를 찾는데 드는 cost를 계산해보자.

 

Case 1. 기본키로 찾는 경우

키본키의 경우 유일성이 보장되기 때문에 조건에 맞는 데이터는 반드시 테이블 당 하나만 존재할 것이다.

따라서 데이터를 찾는 즉시 탐색을 종료해도 된다.

$$ cost = (b_r / 2) \; block \; transfers + 1 \; seek $$

$$ (b_r: \# \; blocks \; from \; relation \;r) $$

 

Case 2. 나머지 경우

linear search시 조건문의 유무, 정렬 여부, 인덱스의 유무과 관계없이 모두 아래와 같은 탐색 시간을 갖는다.

$$ cost = b_r \; block \; transfers + 1 \; seek $$

 

 

아래의 예시에서 다음과 같은 tuple, block수를 사용할 예정.

	student	takes
tuples (n)	5,000	10,000
blocks (b)	100	400
tuples/1 block	50	25

Nested-loop Join Operation

2중 반복문을 돌면서 조건을 검사하고 조건에 맞는 tuple를 결과에 추가하는 join 연산.

여기서 r은 outer relation, s는 inner relation 이라고 한다.

이 연산의 장점은 인덱스도 필요하지 않아서 어떠한 join 연산에서도 사용할 수 있다는 점이다.

하지만, 알고리즘 시간 복잡도가 너무 크고,

특히 inner relation에서 풀스캔이 빈번하게 일어난다(매 루프마다 seek 해야함)

 

- Cost

메모리에는 오직 1블럭만 올릴 수 있다고 가정하자.

$$ (n_r \times b_s + b_r) \; block \; transfers + (n_r + b_r) \; seeks $$

*transfer

여기서 nr * bs는  inner relation에서의 block transfer를 나타낸다.

그 이유는, 한 번의 loop에서 s relation을 모두 탐색하기 위해선 bs의 블럭을 읽어야 하는데,

그 반복문이 nr번 반복되기 때문이다.

br은 outer relation에서의 block transfer를 나타낸다.

*seek

nr은 inner relation의 seek 수를 나타낸다.

그 이유는, 매 루프마다 inner relation이 기록된 곳으로 디스크 헤더를 옮겨야 하기 때문이다.

br은 outer relation의 seek 수를 나타낸다.

그 이유는, inner loop 종료 후 outer relation의 특정 block으로 헤더를 옮겨야 하기 때문이다.

bn이 아닌 이유는, 헤더를 한 번 옮길 때 블럭을 모두 읽어와서 메모리에 올리기 때문이다.

 

r, s 중 크기가 작은 relation이 메모리에 전부 들어갈 수 있는 경우

비용은 다음과 같이 감소한다.

$$ (b_s + b_r) \; block \; transfers + 2 \; seeks $$

 

- Optimize

Case 1. student를 outer relation으로 넣는 경우

$$ 5,000 \times 400 + 100 = 2,000,100 \; block \; transfers $$

$$ 5,000 + 100 = 5,100 \; seeks $$

 

Case 2. takes를 outer relation으로 넣는 경우

$$ 10,000 \times 100 + 400 = 1,000,400 \; block \; transfers $$

$$ 10,000 + 400 = 10,400 \; seeks $$

 

Ts, Tt의 시간을 고려하여 효율적인 방법을 선택한다.

 

Block Nested-loop Join Operation

Nested-loop Join보다 효율적이다.

seek의 횟수가 눈에띄게 감소하기 때문이다.

(위 cost 식에서 nr이 br로 감소하는 효과가 있음)