DBMS - B+Tree

Index

인덱스는 table의 attribute의 부분집합을 복제하여 구조화, 정렬한 것으로 빠른 접근을 가능케 한다.

따라서 attribute로 만들 수 있는 모든 조합의 집합으로 인덱싱 해놓으면

어떻게 검색을 하든 매우 빠르게 데이터를 찾을 수 있을 것이다.

하지만, 이런 경우에는 저장공간이나, 업데이트시에 오버헤드가 매우 커지기 때문에 현실적으론 불가능하다.

 

따라서 공간 효율적으로 인덱싱 하기 위해 자료구조를 잘 사용해야 하는데,

이번 포스팅의 주제인 B+Tree는 DBMS에서 사용하기에 매우 적합한 자료구조이다.

 

B+Tree

B-Tree는 BST의 밸런싱 문제를 해결하고자 나온 자료구조인데,

B+Tree는 이런 B-Tree의 특성을 살리면서 데이터베이스 시스템에서 사용하기 좋게

기능이 추가된 버전이라 할 수 있다.

 

왜 DBMS에서 사용하기 좋은가 하면은,

데이터베이스는 가용 메모리보다 큰 양의 데이터를 모두 다뤄야 하기 때문에 디스크 저장장치를 필연적으로 사용해야 한다.

이 때, 디스크는 블럭 단위로 데이터를 저장하는데, B+Tree 역시 블럭 단위로 데이터(노드)를 관리한다.

따라서 메모리에서만 동작할 때는 B+Tree보다 좋은 알고리즘이 있겠지만,

디스크에서 동작할 때는 B+Tree만큼 좋은 알고리즘을 찾기 어렵다.

 

B+Tree의 특징으로는 self-balancing tree로 모든 leaf-node의 depth가 같을 뿐만 아니라,

hash table의 문제였던 범위 탐색도 가능하다는 점이다.

뿐만 아니라 이런 강력한 성능을 갖고 있음에도 데이터 삽입/변경/삭제/탐색이 모두 O(log n)의 시간복잡도를 갖는다.

 

이런 특징을 갖기 위해서 B+Tree를 구성하는 노드의 제약사항이 따르는데,

각 노드는 M개의 자식 노드를 가질 수 있다고 할 때,

root node를 제외한 나머지 노드는 아래와 같은 key의 개수의 제한을 갖는다.

$$ M/2-1 \leq \#Keys \leq M-1 $$

노드마다 key의 최소 개수의 제한이 있는 이유는 두 가지 이유가 있다.

• Disk access시 블럭 단위로 접근하는데, 원소 개수가 너무 적으면 비효율적이기 때문
• Depth가 너무 깊어지는 것을 방지

 

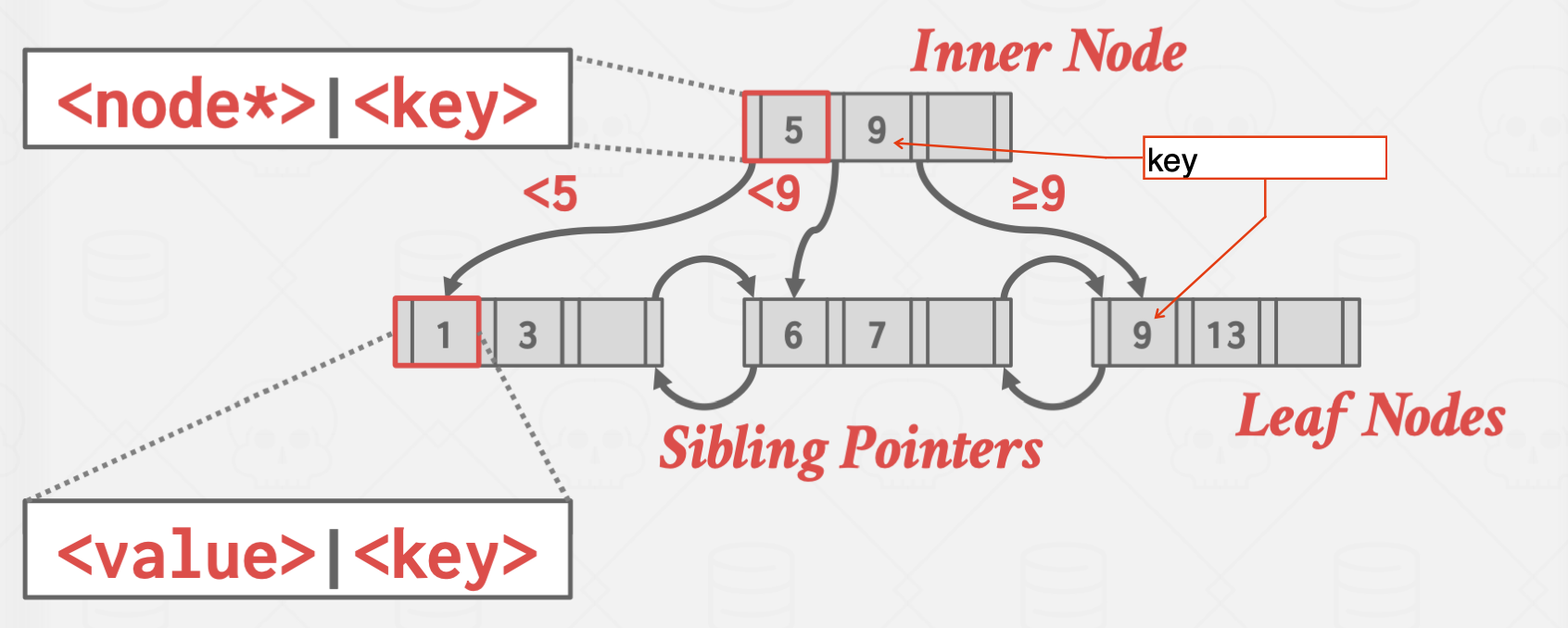
B+Tree는 B-Tree와 다르게 Inner Node에는 값이 저장되지 않는다.

그렇게 함으로써 모든 값들은 Leaf Node에만 저장되도록 할 수 있고,

각 노드에 들어갈 수 있는 키값이 많아지기 때문에 depth를 줄일 수 있다.

또한 Leaf Node는 Sibling Pointer가 존재하기 때문에 옆의 블럭을 읽어올 때

부모 노드를 다시 읽어오는 일이 없어 DIsk access를 줄일 수 있다.

 

Leaf Node에 들어갈 값이 너무 큰 경우, 즉, 한 메모리 공간에 값을 저장하기 어려운 경우에는

값이 저장된 곳의 주소를 저장하는 방법을 채택하기도 한다.

값(튜플)이 크지 않더라도 튜플 자체를 저장하는 것이 아닌, 튜플의 record ID를 저장하기도 하는데,

각 방법에는 장단점이 존재한다.

 

value 저장 데이터	Record ID	Tuple Data
의미	tuple이 저장된 곳의 위치 포인터를 저장 이 경우에 key 값으로 record ID를 사용한다.	실제 tuple값을 저장 이 경우에 key 값으로 기본키를 사용한다.
장점	인덱스 B+Tree 생성시 key는 인덱스할 attribute를, 값으로 위치 포인터가 저장되기 때문에 어떤 인덱스를 만들더라도 1회만 B+Tree를 탐색하면 주소 접근으로 tuple 값을 가져올 수 있다.	주소가 아닌 실제 튜플값이 저장되어 있기 때문에 B+Tree를 탐색만 하면 더이상의 Disk access가 필요 없다.
단점	B+Tree를 탐색 하더라도 값이 아닌 주소가 있기 때문에, 탐색시간이 길어질 수 있다.	인덱스 B+Tree 생성시 key는 인덱스할 attribute를, 값으로 기본키를 저장하기 때문에 B+Tree를 2회 탐색 해야지만 데이터를 가져올 수 있다.

 

반대로 키값이 가변적인 길이를 갖는 경우 아래와 같은 방법들로 해결할 수 있다

• tuple의 attribute의 포인터로써 키값을 저장
• 가변길이의 Node를 사용 (거의 사용 안 함)
• 제일 긴 키에 맞추어 공간을 할당하고 모든 키에 Padding을 주는 방법
• key를 hash table를 사용하여 저장

 

Insert / Delete

데이터 추가시에는 빈 공간이 있으면 그냥 데이터를 넣지만,

빈 공간이 없으면 해당 leaf node를 둘로 나누고 데이터를 넣는다.

 

삭제시에도 데이터가 절반 이상 차있으면 그냥 삭제하지만,

절반보다 작아진다면, 옆의 노드의 키가 많은 경우 옆에서 가져오고,

옆의 노드도 적다면 두 노드를 합친다.

하지만, 데이터를 삭제하고 바로 추가하는 경우, merge할 때 오버헤드가 크기 때문에

성능상의 이유로 데이터가 절반 이하로 떨어졌다고 해서 바로 노드를 수정하는게 아닌

최대한 뒤로 미루며 성능 향상을 꾀하기도 한다.

 

B+ Tree Visualization

시각화 툴을 이용하면 더욱 좋습니다.

 

Selection Conditions

B+Tree는 Inner Node의 키 값을 이용해서 탐색할 하위 노드를 결정할 수 있다.

가령 (*, B, *)의 튜플을 찾고싶다고 한다면, 체크 표시인 노드만 탐색해도

누락없이 조건에 맞는 튜플을 찾을 수 있다.

 

Duplicate Keys Problem

중복되는 키 값에 대해 B+Tree에서 해결하는 방법은 크게 두 가지 방법이 있다.

 

- Append Record ID

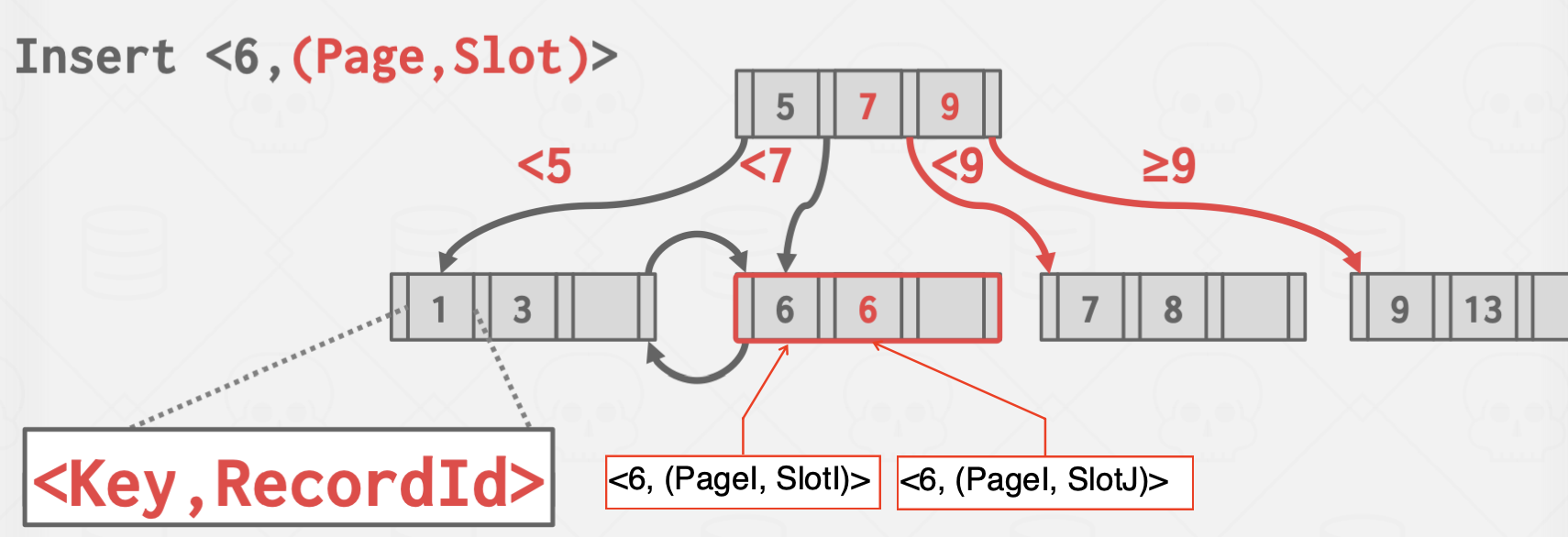
키값에 주소를 붙여 유니크하게 만드는 방법.

 

- Overflow Leaf Node

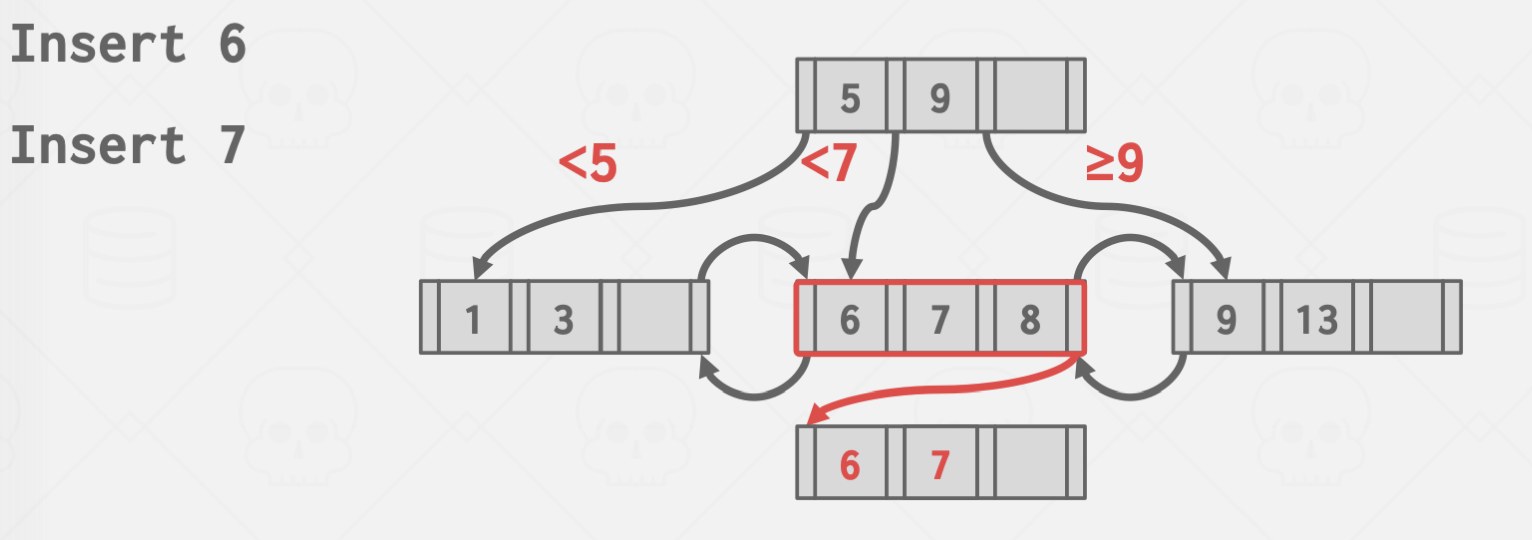
Leaf Node 아래에 중복되는 키를 위한 Overflow Leaf Node를 만드는 방법.

 

Clustered Index, B+Tree

기본키를 기준으로 정렬된 인덱스를 Clustered Index라고 부른다.

 

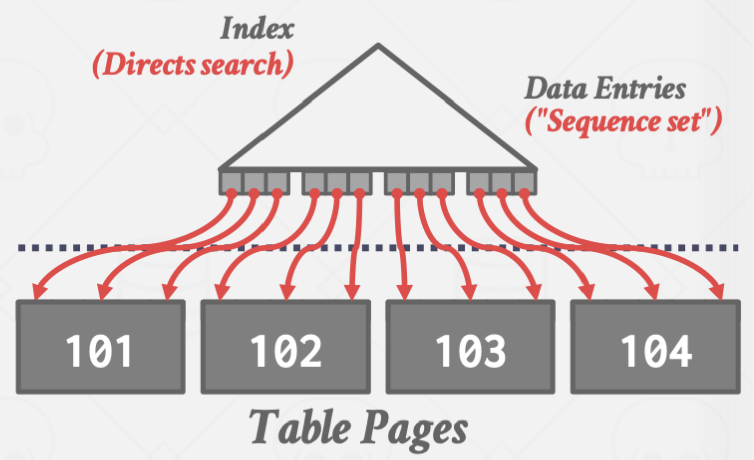
Clustered B+Tree는 순차탐색시 페이지를 한 번만 로드하면 모든 데이터를 가져올 수 있기에

DIsk I/O 부분에서 오버헤드가 적다.

 

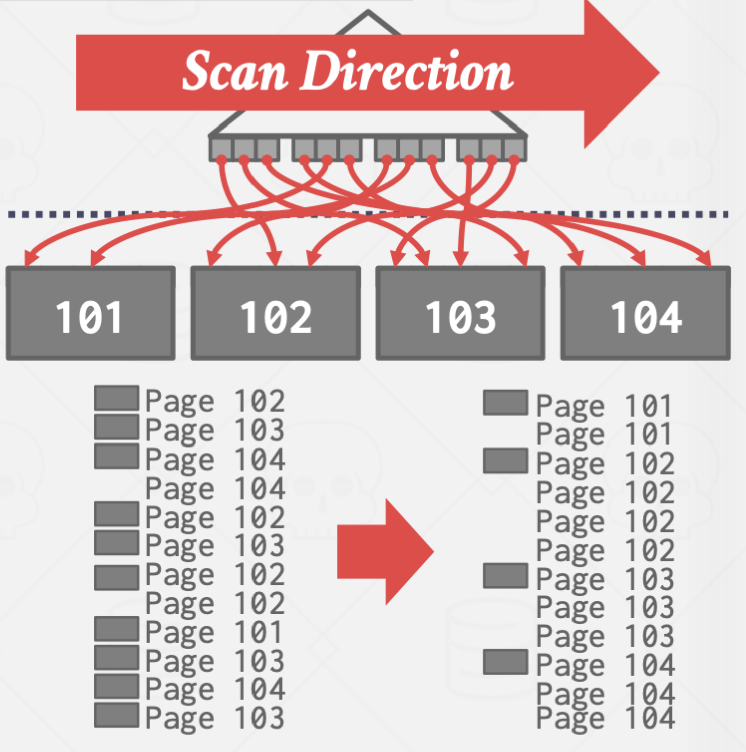
그렇지 않은 경우에는 순차탐색시 한 페이지를 여러번 로드해야 할 상황이 생기는데,

이를 방지하기 위해 DBMS는 실제로 페이지를 읽지 않고 분석하여 읽을 페이지를 정렬하고 읽기도 한다.