Tips for Divide and Conquer

Thresholds

Merge Sort, Exchange Sort를 예로 들어보자.

merge sort의 time complexity는 n lg n 이었다.

exchange sort는 이중 반복문을 통한 정렬 방법으로 n^2의 time complexity를 갖는다.

 

대부분의 경우에는 merge sort를 사용하는 것이 더 시간이 적게 걸릴 것이다.

하지만, n의 크기가 작은 경우에는 exchange sort를 사용하는 것이 더 효율적일 수 있다.

 

그 이유는 merge sort가 동작함에 있어 아래와 같은 기능은 오버헤드가 있기 때문이다.

• mid 계산
• 재귀함수 호출 시, call stack에 2개의 함수를 추가
• 2개의 subArray를 merge

 

따라서 Thresholds를 정해 입력의 갯수 n이 특정 수 이하로 내려갈 경우

merge sort를 실행하는 것 보다 exchange sort를 사용하는 것이 더 효율적인 구현일 것이다.

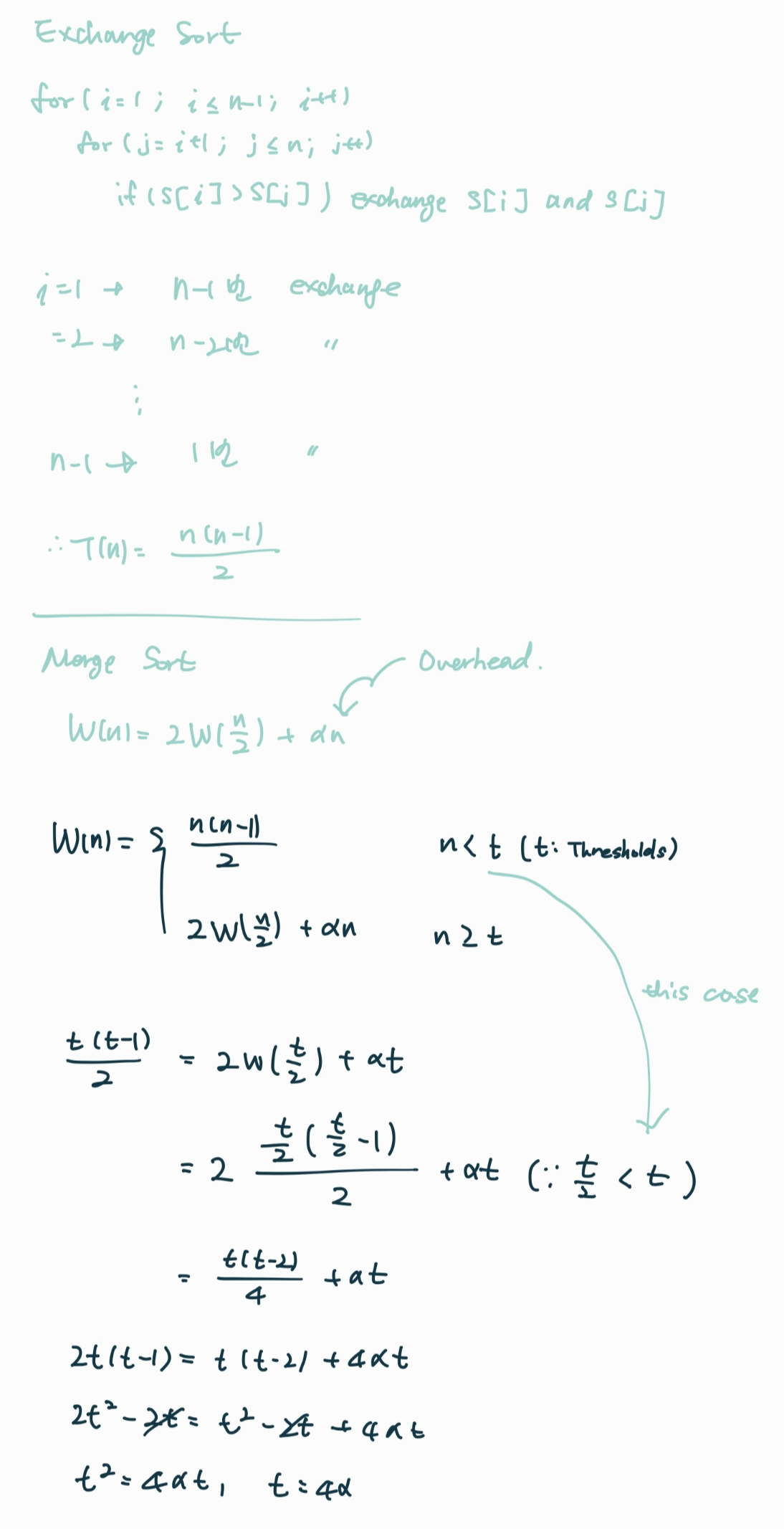
이 경우에는 n의 크기가 4a보다 작으면 exchange sort를 실행하는게 더 빨라진다.

 

 

Bad case for Divide and Conquer

다음과 같은 경우에는 분할 정복 방법이 오히려 역효과가 날 수 있다.

• 분할된 인스턴스(배열)가 본래 크기와 별반 다르지 않을 때
• 분할된 인스턴스의 수가 본래 크기과 별반 다르지 않을 때 (즉, 인스턴스 크기가 1에 가까울 때)

 

피보나치 수열을 재귀 함수로 구현한 경우가 바로 이 경우이다.