Quick Sort

* 배열의 인덱스가 1부터 시작한다고 가정합니다.

([1] = 1번째 와 같이 이해하기 쉽도록)

 

- 알고리즘 정의

기본적인 방식은 Merge Sort와 동일하다.

다만, 배열을 반으로 분해하는 것이 아닌, 배열 내부에서 원소의 위치를 이동시키기 때문에

Combine part가 필요가 없어진다.

(붉은 원이 pivotItem,

pivotItem보다 √ 가 작을 경우 ++j와 √ 의 위치를 변경,

마지막에 pivotItem과 j의 위치를 변경,

위 과정을 재귀 호출)

 

- Pseudocode

// S: global
public static void quickSort (index low, index high) {
    if (high <= low) return;
    
    int pivotPoint = partition(low, high);
    quickSort(low, pivotPoint - 1);
    quickSort(pivotPoint + 1, high);
}

public static void partition (index low, index high) {
    index i, j, pivotPoint;
    keyType pivotItem;
    
    pivotItem = S[low];
    j = low;
    
    for (i = low+1; i <= high; i++) {
        if (S[i] < pivotItem) exchange S[i] and S[++j]
    }
    pivotPoint = j;
    exchange S[low] and S[pivotPoint];
    
    return pivotPoint;
}

pivotPoint는 재귀 호출시 배열을 분할할 인덱스를 가리킨다.

이 때, pivotPoint를 기준으로 왼쪽은 pivotItem보다 작은 원소만이 정렬되지 않은 상태로 배열에 있고,

오른쪽은 보다 큰 원소만이 정렬되지 않은 상태로 배열에 있다.

이 pivotPoint를 알아내기 위해 partition 함수를 사용한다.

partition은 입력으로 들어온 배열의 범위 low ~ high 에서 S[low]를 pivotItem 삼아

S[low]를 기준으로 작은/큰 원소를 좌/우로 분리하는 과정을 마친 후,

정렬된 pivotItem의 index, 즉, pivotPoint를 반환하는 역할을 수행한다.

 

- Time complexity (partition part)

Basic Operation: S[i] < pivotItem

Input Size: high - low + 1 (sizeof SubArray of S)

 

* Every case: T(m) = m - 1

 

- Time complexity (quickSort part)

Basic Operation: call partition

Input Size: n

 

* Best case:

[Θ(n lg n)]

 

* Worst case:

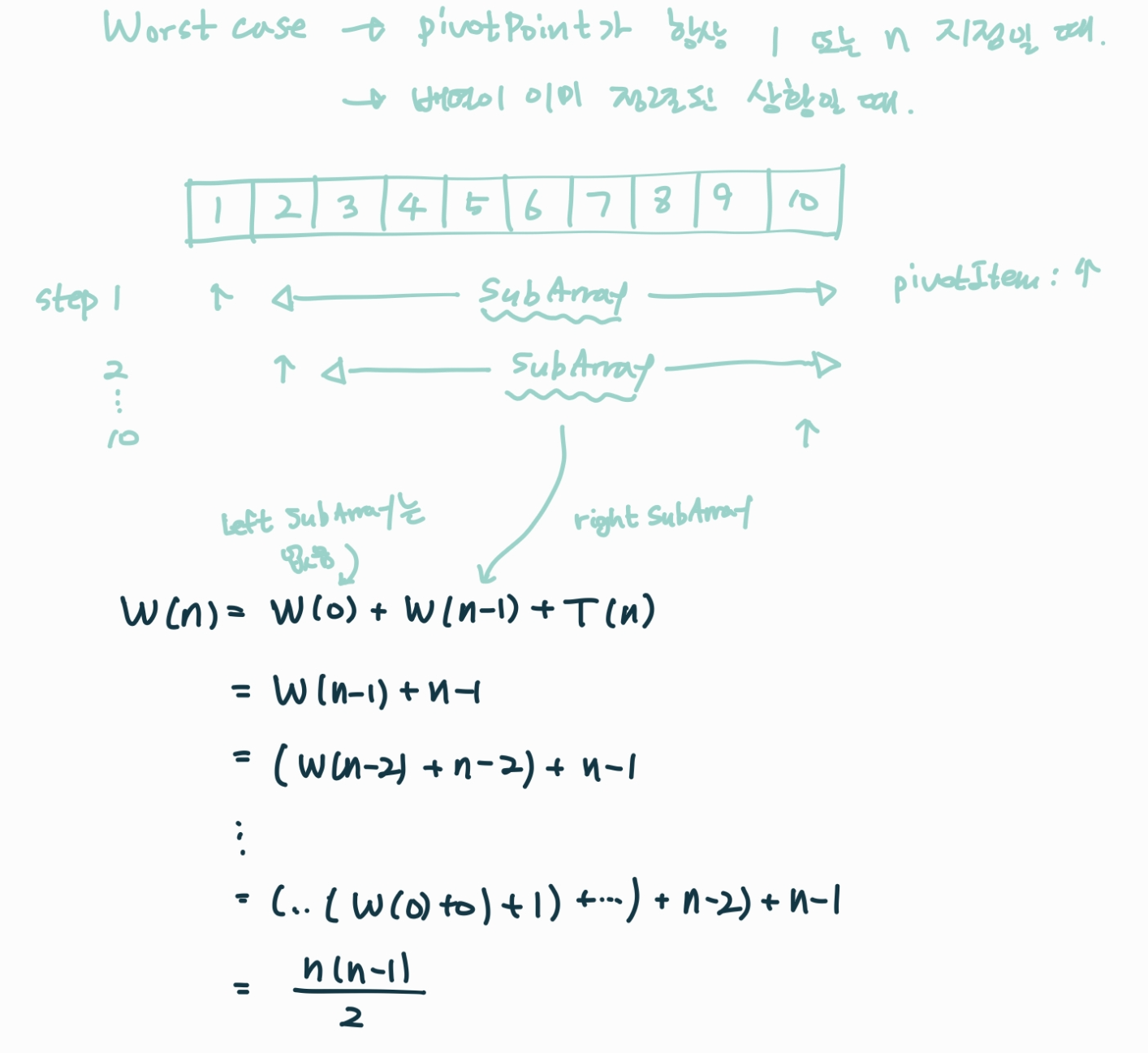
[Θ(n^2)]

 

* Average case:

[Θ(n lg n)]