-
- 그래프
노드와 노드를 연결하는 간선들로 이루어진 비 선형 자료구조로 트리와 다르게 패턴이 없다.
모든 노드가 1-1로 연결되어 있는 그래프를 완전 그래프 (Complete Graph)라 부르고,
원래 그래프에서 일부 간선을 제외한 그래프를 부분 그래프 (Subgraph)라 부른다.
그래프의 표현 방법은 인접 행렬 (Adjacency Matrix)과 인접 리스트 (Adjacency List)로 표현할 수 있는데,
인접 행렬로 표현시 구현이 쉽고, 특정 노드간의 인접 여부 확인이 빠르다는 장점이 있지만,
특정 노드와 인접한 모든 노드를 알고자 할 때, 모든 간선을 확인해야 하고,
구현상의 이유로 메모리 낭비가 발생한다는 단점이 있다.
반면에 인접 리스트로 표현시 메모리 효율적이고, 인접한 노드를 효율적으로 할 수 있지만,
특정 노드간의 인접 여부 확인이 느리다는 단점이 있다.
인접 행렬로 그래프를 구현해보자.

Graph.hpp 
Graph.cpp 
main.cpp 
- 그래프 순회
하나의 노드에서 시작해 모든 노드를 탐색하는 방법에는 크게 두 가지 방법이 존재한다.
1. 깊이 우선 탐색 (Depth First Search)

Graph.cpp 추가 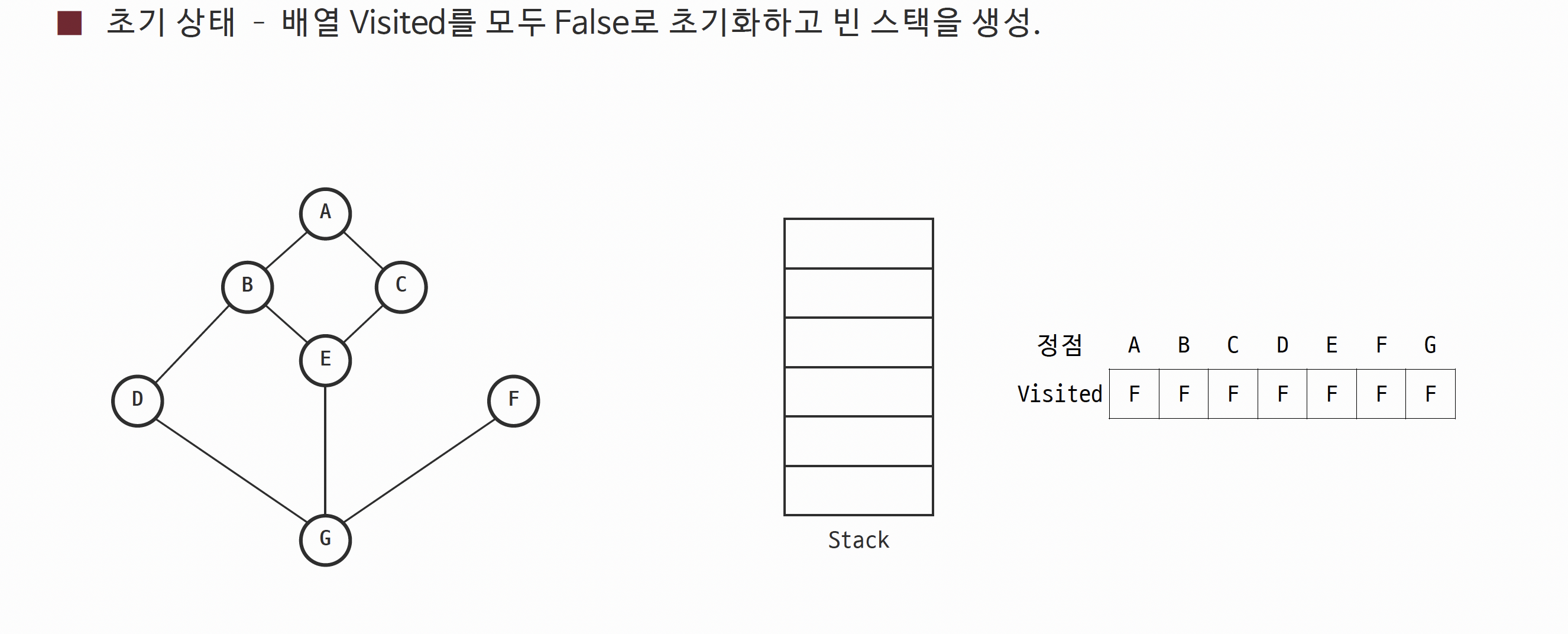











2. 너비 우선 탐색 (Breadth First Search)













- 다익스트라 알고리즘 (Dijkstra Algorithm)
음이 아닌 가중치를 갖는 가중 그래프에서 한 노드에서 다른 모든 노드까지의 최단거리를 구하는 알고리즘.







