Graph

Graph

그래프는 트리와 마찬가지로 비 선형적 자료구조로

node와 노드를 잇는 link의 집합으로 구성된다.

트리와 가장 큰 차이점은 그래프의 노드는 어떠한 패턴으로 연결되도 상관 없다는 것이다.

(심지어 비어있거나, 연결이 아예 안된 노드도 존재할 수 있음)

 

노드의 구현과 탐색에 앞서 노드의 용어부터 정리하고 가자.

<Fig. 01: Undirected / Directed graph>

Path: vertex들의 순서나열.

e.g. path of v0 to v2: e0 e1 / e0 e2 e3 e5 / e4 e5 / e4 e3 e2 e1

Cycle: 출발 vertex = 도착 vertex인 path

Multiple edges: 같은 두 vertex 사이 2개 이상의 edge가 연결된 것.

Simple Graph: loop, multiple edges가 없는 graph

 

<Fig. 02: example graph>

위 그래프를 나타내는 노드의 구현은 크게 세 가지 방법이 존재한다.

1. Adjacency Matrix

<Fig. 03: adjacency matrix implement <Fig. 02>>

cell[i][j]는 vertex i에서 j로의 연결을 표현하고, T는 연결되어 있음을 의미한다.

T 대신 숫자가 들어간 경우 해당 연결 사이의 weight을 나타낸다.

 

2. Adjacency List

<Fig. 04: adjacency list implement <Fig. 02>>

cell[i]는 vertex i에 직접적으로 연결되어 있는 vertex들이 linked list형태로 저장되어 있다.

 

3. Edge Set

<Fig. 05: edge set implement <Fig. 02>>

cell[i]는 vertex i에 직접적으로 연결되어 있는 vertex들이 set형태로 저장되어 있다.

 

 

이 포스트에서는 비교적 간단한 Adjacency Matrix를 이용한 graph를 구현해볼 것이다.

template <class Item>
class graph { 
    public: 
        …
        static const std::size_t MAX = 20;
    private:
        bool edges[MAX][MAX];
        Item labels[MAX];
        std::size_t many_vertices;
}

 

template <class Item>
Item &graph<Item>::operator[](std::size_t vertex) {
    assert(vertex < size());
    return labels[vertex];
}

일단 인덱스에 접근하기 위해 operator overloading을 구현해준다.

 

template <class Item>
void graph<Item>::add_vertex (const Item &label) {
    std::size_t new_vertex_number;
    std::size_t vertex;
    assert(size() < MAX);
    new_vertex_number = many_vertices;
    ++many_vertices;
    for (vertex = 0; vertex < many_vertices; ++vertex) {
        edges[vertex][new_vertex_number] = false;
        edges[new_vertex_number][vertex] = false;
    }
    labels[new_vertex_number] = label;
}

<Fig. 06: add_vertex>

vertex를 추가하는 함수.

lables에 값을 넣어주고, edges를 false로 초기화한다.

 

template <class Item>
void graph<Item>::add_edge(std::size_t source, std::size_t target) {
    assert(source < size());
    assert(target < size());
    edges[source][target] = true;
}

template <class Item>
void graph<Item>::remove_edge(std::size_t source, std::size_t target) {
    assert(source < size());
    assert(target < size());
    edges[source][target] = false;
}

template <class Item>
bool graph<Item>::is_edge(std::size_t source, std::size_t target) const {
    assert(source < size());
    assert(target < size());
    return edges[source][target];
}

edge의 setter, getter 함수.

 

template <class Item>
std::set<std::size_t> graph<Item>::neighbors(std::size_t vertex) const {
    std::set<std::size_t> answer;
    std::size_t i;
    assert(vertex < size());
    for (i = 0; i < size(); ++i) {
        if(edges[vertex][i])
            answer.insert(i);
    }
    return answer;
}

vertex에 연결되어있는 vertex의 집합을 리턴하는 함수.

 

 

Graph Traversal

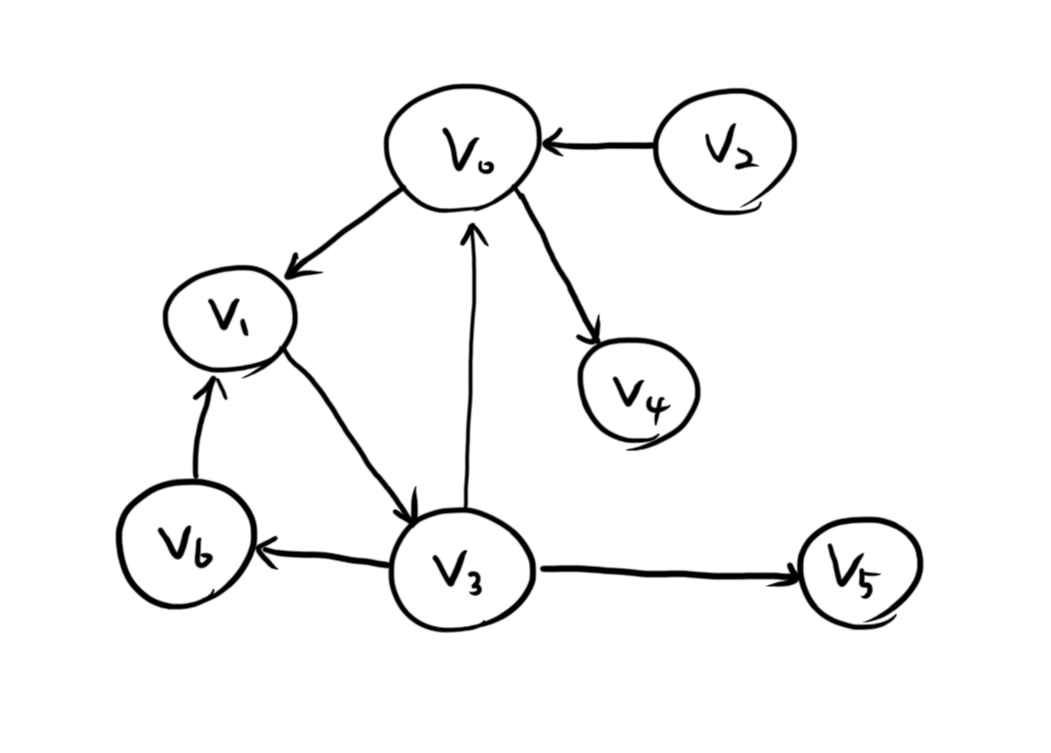
<Fig. 07: example graph>

그래프를 탐색하는 방법은 크게 두 가지 방법이 있다.

1. Depth-first Search

재귀방식으로 탐색하는 방법으로 하나의 이웃을 우선 깊게 탐색하는 방법이다.

template <class Process, class Item, class SizeType>
void depth_first (Process f, graph<Item> &g, SizeType start) {
    bool marked[g.MAX];
    assert(start < g.size());
    std::fill_n(marked, g.size(), false);
    
    rec_dfs(f, g, start, marked);
}

template <class Process, class Item, class SizeType>
void rec_dfs(Process f, graph<Item> &g, SizeType v, bool marked[]) {
    std::set<std::size_t> connections = g.neighbors(v);
    std::set<std::size_t>::iterator it;
    marked[v] = true;
    f(g[v]);  // traversal
    for (it = connections.begin(); it != connections.end(); ++it) {
        if (!marked[*it])
            rec_dfs(f, g, *it, marked);
    }
}

위 코드를 통해 Depth-first Search를 구현할 경우 아래와 같이 모든 vertex를 탐색하게 된다.

<Fig. 07>: v0 v1 v3 v5 v6 v4

 

2.  Breadth-first Search

queue를 활용한 탐색 방법으로 여러 이웃을 골고루 탐색하는 방법이다.

template <class Process, class Item, class SizeType>
void breadth_first (Process f, graph<Item> &g, SizeType start) {
    bool marked[g.MAX];
    std::set<std::size_t> connections;
    std::set<std::size_t>::iterator it;
    std::queue<std::size_t> vertex_queue;
    assert(start < g.size());
    std::fill_n(marked, g.size(), false);
    
    marked[start] = true;
    f(g[start]);  // traversal
    vertex_queue.push(start);
    do {
        connections = g.neighbors(vertex_queue.front());
        vertex_queue.pop();
        for (it = connections.begin(); it != connections.end(); ++it) {
            if (!marked[*it]) {
                marked[*it] = true;
                f(g[*it]);  // traversal
                vertex_queue.push(*it);
            }
        }
    } while (!vertex_queue.empty());
}

위 코드를 통해 Breadth-first Search를 구현할 경우 아래와 같이 모든 vertex를 탐색하게 된다.

<Fig. 07>: v0 v1 v4 v3 v5 v6

 

 

Path Arlgorithm

위에서 본 DFS, BFS의 방식은 vertex u, v 사이가 연결되어있는가를 확인하는 알고리즘이다.

v에 한 번이라도 방문했다면, u-v는 연결되어있다는 뜻이다.

하지만 vertex사이 edge에 weight가 있고, 두 vertex사이에 최소거리,

즉 weight의 합이 최소가 되는 경로를 찾는 방법은 무엇일까?

start vertex에서 연결된 모든 vertex의 최소거리를 구하는 대표적인 알고리즘에는 Dijkstra Algorithm이 있다.

 

pseudo code의 일부를 살펴보자.

for (v = 0; v < n; v++) {
    if ((v is not in allowed_vertex) && (there is an edge from next to v)) {
        sum = distance[next] + weight(next, v)
        if (sum < distance[v]) {
            distance[v] = sum
            predecessor[v] = next
        }
    }
}

하나의 vertex에서 next vertex 사이의 거리를 계산하는데,

새로 계산된 거리가 기존에 저장된 거리보다 짧을 경우 갱신하는 과정으로 구현된다.

 

이 때, predecessor에 최소거리가 되는 vertex사이의 관계를 저장 및 갱신하는데,

특정 vertex에서 start vertex까지의 최단경로가 되게 하는 vertex의 연결 관계를 출력하려면 다음과 같이 하면 된다.

vertex = v;
cout << vertex << endl;
while (vertex != start) {
    vertex = predecessor[vertex];
    cout << vertex << endl;
}

이렇게하면 역순으로 vertex의 연결관계를 출력할 수 있다.

정순으로 출력하려면 출력대신 stack에 넣어주고, 마지막에 stack이 빌 때 까지 출력하며 pop하면 될 것이다.