Tree

트리구조는 아주 중요한 알고리즘이라 세 번에 나누어서 진행할 예정이다.

 

Tree... 이게 얼마나 사기(?)냐 하면은 트리를 이용하여 데이터를 관리할 경우

데이터 탐색에 필요한 시간이 O(n^2)에서 O(nlogn)까지 감소할 수 있다.

즉, array는 최악의 경우 특정 데이터를 찾는데 100만 번의 비교(약 16.6분)가 필요하다면,

Tree(그 중에 binary heap)은 단 20번이면 비교(20밀리초)가 끝난다.

 

트리구조를 알아보기 앞서 용어부터 정리하자.

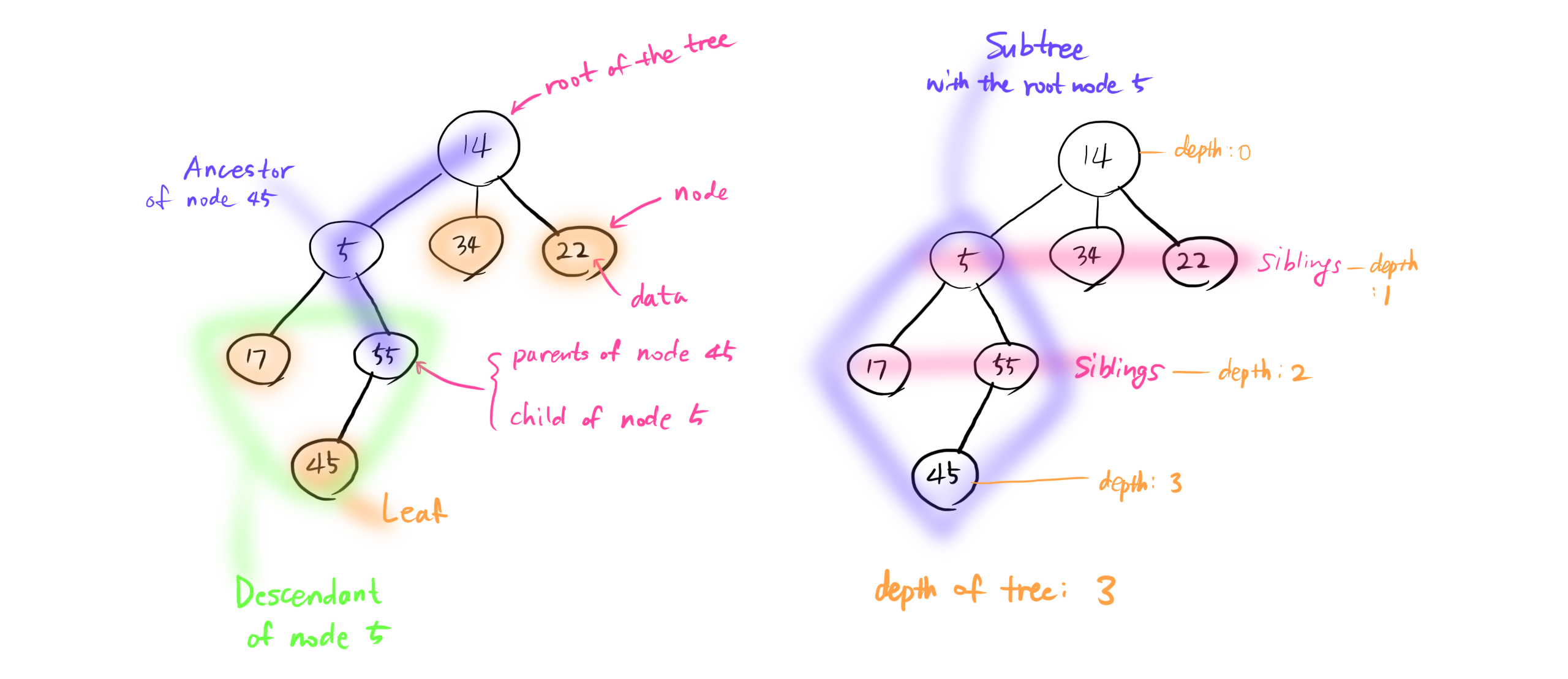
<Fig. 01: tree definitions>

Tree: node들의 무한 집합

Root: Parent node가 없는 최상단의 노드

Parent: node위에 연결된 노드

Child: node아래에 연결된 노드

Sibling: Parent node가 같은 노드

Leaf: Child node가 없는 최하단의 노드

Ancestor: Root까지 올라가는 Parent node의 집합

Descendant: 모든 Leag까지 내려가는 Child node의 집합

Subtree: 기존 Tree에서 떼어냈을 때, 또 하나의 Tree가 생성될 때의 그 집합

Depth of a node: Root node에서 떨어진 정도

Depth of the tree: 가장 깊은 depth를 가진 leaf node의 depth

 

 

Tree의 종류

1. Binary Tree

각 노드가 최대 2개의 자식노드를 갖는 트리구조.

 

2. Full Binary Tree

Binary Tree 중, 모든 리프노드가 같은 depth를 갖는 트리구조.

즉, 리프노드가 아닌 모든 노드는 2개의 자식노드를 갖는다. (노드의 갯수: 2^(depth+1)-1)

 

3. Complete Binary Tree

Binary Tree 중, 왼쪽부터 차곡차곡 채워나간 트리구조.

가장 깊은 depth를 제외한, 각 depth의 노드의 갯수는 2^depth개 이고,

가장 깊은 depth를 갖는 리프노드는 왼쪽부터 채워져있다.

따라서 노드의 갯수가 정해지면 CBT의 모양은 하나로 결정된다.

 

Complete Binary Tree의 장점은 비선형 구조인 tree를 선형 구조인 array로 표현할 수 있다는 점이다.

root node의 데이터는 [0]에 저장하고,

각 node의 데이터는 [i]에 저장한다고 했을 때,

왼쪽 자식은 [2i+1], 오른쪽 자식은 [2i+2]에 저장된다.

 

4. Binary Search Tree

Binary Tree 중, 루트노드의 왼쪽 서브트리의 노드는 루트노드보다 작거나 같아야 한다.

루트노드의 오른쪽 서브트리의 노드는 루트노드보다 커야한다.

이게 완전 중요!

그래서 별도의 포스팅으로 진행.

Tree - Binary Search Tree

 

 

 

Binary Tree에 사용할 Node 구현

template<class Item>
class binary_tree_node { 
    …
    private:
        Item data_field;
        binary_tree_node *left_field;
        binary_tree_node *right_field;
};

데이터를 저장할 data_field와, 왼쪽, 오른쪽 자식 노드를 연결할 link field 들로 구성된다.

 

binary_tree_node(const Item &init_data = Item(),
	binary_tree_node *init_left = NULL,
	binary_tree_node *init_right = NULL) {
    data_field = init_data;
    left_field = init_left;
    right_field = init_right;
}

생성자 함수.

init_data의 기본값이 함수 형태인 이유는, reference 타입으로 인자를 넘기는 경우, 변수가 인자로 넘어오기 때문에,

익명의 변수를 만들어주는 효과를 내기 위함이다.

 

Item &data() {  // n->data() = 42;
    return data_field;
}

const Item &data() const {
    return data_field;
}

binary_tree_node *&right() {  // n->right() = q;
    return right_field;
}

const binary_tree_node *left() const {
    return left_field;
}

data, link field getter함수. 단, &를 사용하여 대입 연산자를 사용할 수 있도록 구현.

 

void set_data(const Item &new_data) { 
    data_field = new_data; 
}

void set_right(binary_tree_node *new_right) { 
    right_field = new_right; 
}

data, link field setter함수.

 

bool is_leaf() const {
    return (left_field == NULL && right_field == NULL);
}

해당 node가 리프노드인지 확인하는 함수.

 

template <class Item>
void tree_clear(binary_tree_node<Item> *&root_ptr) {
    if (root_ptr != NULL) {
        tree_clear(root_ptr->left());
        tree_clear(root_ptr->right());
        delete root_ptr;
        root_ptr = NULL;
    }
}

binary tree를 비워주는 함수.

루트 노드의 포인터를 인자로 넣으면 트리(혹은 서브트리)의 모든 노드를 삭제한다.

인자로 들어온 포인터가 NULL이 아니라면, 왼쪽 서브트리, 오른쪽 서브트리를 재귀적으로 삭제하고,

인자로 들어온 본인을 삭제한다.

 

binary_tree_node<Item> *tree_copy(binary_tree_node<Item> *root_ptr) {
    binary_tree_node<Item> *l_ptr;
    binary_tree_node<Item> *r_ptr;
    
    if (root_ptr == NULL)
        return NULL;
    else {
        l_ptr = tree_copy(root_ptr->left());
        r_ptr = tree_copy(root_ptr->right());
        return new binary_tree_node<Item>(root_ptr->data(), l_ptr, r_ptr);
    }
}

binary tree를 복사하는 함수.

루트 노드의 포인터를 인자로 넣으면 트리(혹은 서브트리)의 모든 노드를 복사한다.

인자로 들어온 포인터가 NULL이 아니라면, 왼쪽 서브트리, 오른쪽 서브트리를 재귀적으로 복제한 후,

이진 트리 노드의 생성자 함수를 이용해서 루트노드를 만들고 왼쪽 서브트리, 오른쪽 서브트리를 연결한다.

인자로 들어온 포인터가 NULL이라면 NULL을 리턴한다.

(이후에 생성자 함수로 노드를 만들 때, 서브트리 부분이 자동으로 NULL로 들어가게 된다)

 

 

Binary Tree 탐색

<Fig. 02: (Full) Binary Tree example>

1. pre-order traversal

루트노드를 탐색하고, 왼쪽 서브트리, 오른쪽 서브트리를 재귀적으로 탐색하는 방법이다.

탐색결과: * + 3 y - 2 x

 

2. in-order traversal

왼쪽 서브트리를 재귀적으로 탐색하고, 루트노드를 탐색하고, 오른쪽 서브트리를 재귀적으로 탐색하는 방법이다.

탐색결과: 3 + y * 2 - x

 

3. post-order traversal

왼쪽 서브트리, 오른쪽 서브트리를 재귀적으로 탐색하고 루트노드를 탐색하는 방법이다.

탐색결과: 3 y + 2 x - *

 

template <class Item>
void preorder_print(const binary_tree_node<Item> *root_ptr) {
    if (root_ptr != NULL) {
        cout << root_ptr->data() << endl;  // Print
        preorder_print(root_ptr->left());
        preorder_print(root_ptr->right());
    }
}

위 코드는 pre-order traversal의 구현 코드인데,

Print 라인의 코드와 재귀함수 호출 위치에 따라 1~3번 탐색방법 모두 구현 가능하다.

 

 

Function Parameter

만약, 탐색을 진행하면서 수행할 기능의 종류가 100개 있다고 가정해보자.

그렇다면 위의 탐색 코드에 수행할 기능을 추가하여 총 100개의 탐색 코드를 구현해야 할 것이다.

이는 매우 귀찮을 것이다.

따라서 함수의 인자로 함수 파라미터를 넘겨주는 방법을 사용하는게 좋다.

(즉, 1개의 탐색 코드와 100개의 기능구현 함수만 구현하면 된다)

void apply(void f(int &), int data[], size_t n) {
    size_t i;
    for (i=0; i<n; i++)
        f(data[i]);
}

void add1(int &i) { i += 1; }
void triple(int &i) { i *= 3; }


// template version
template <class Item, class SizeType>
void apply(void f(Item &), Item data[], SizeType n) {
    SizeType i;
    for (i=0; i<n; i++)
        f(data[i]);
}

void add1(int &i) { i += 1; }
void toUpperCase(char &c) { c = toupper(c); }


// a more general template version
template <class Process, class Item, class SizeType>
void apply(Process f, Item data[], SizeType n) {
    SizeType i;
    for (i=0; i<n; i++)
        f(data[i]); // f can be called with a single Item argument
}

void add1(int &i) { i += 1; }
void print(double d) { cout << d << endl; }


// using
int[10] n = {1, 2, 3, ...};
apply(add1, n, 10);

 

이런 방식으로 위에 구현했던 Binary Tree 탐색코드를 다시짜보면 다음과 같아진다.

template <class Process, class BTNode>
void preorder(Process f, BTNode *node_ptr) {
    if (node_ptr != NULL) {
        f(node_ptr->data());
        preorder(f, node_ptr->left());
        preorder(f, node_ptr->right());
    }
}