Arithmetic for Computer

Overflow (Underflow)

overflow 현상은 다음과 같은 상황에 발생한다.

$$ ve + ve $$

$$ -ve +  (-ve) $$

$$ ve - (-ve) $$

$$ -ve - ve $$

overflow가 발생하지 않도록 연산에 유의하거나,

발생했을 때 별도의 처리를 해 줘야 한다.

이미지, 영상 처리과 같은 곳에서는 Satrating operations 과정을 거치는데,

간단하게 말하면, overflow가 발생한 경우, 표현 가능한 최대의 숫자로 값을 바꾸는 것을 의미한다.

 

 

Multiplication (H/W)

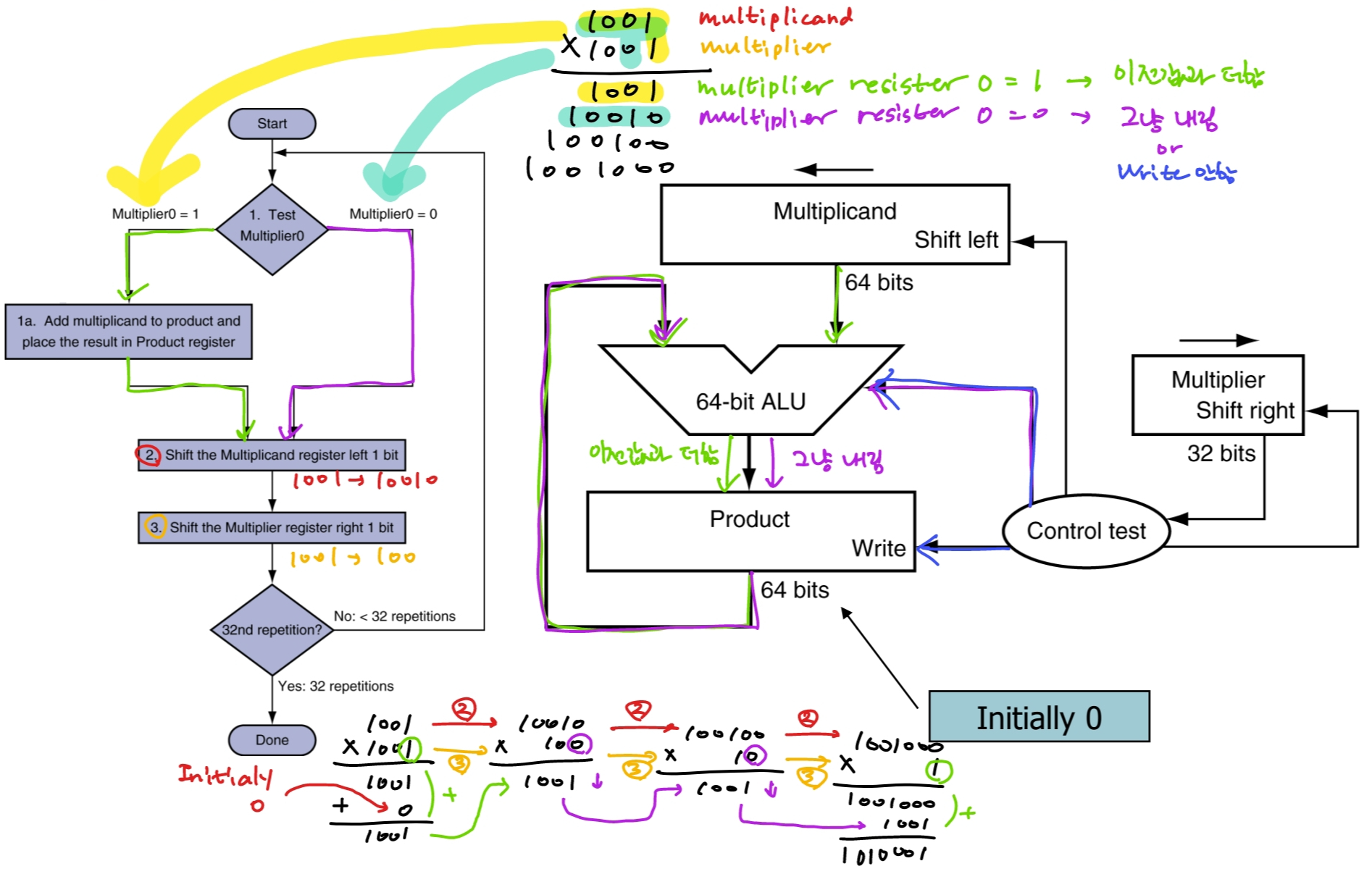
하드웨어 레벨에서의 곱셈을 하는 방식은 위 그림과 같다.

1001 * 1001 의 연산을 예로 들어보자.

1. multiplier의 가장 낮은 bit가 1인 경우,
   product register에 있던 값과 multiplicand의 값을 더하고 그 값을 product register에 저장한다.
2. multiplier의 가장 낮은 bit가 0인 경우,
   product register의 값을 더하지 않고 그냥 내린다.
3. multiplicand register를 1 bit 왼쪽으로 shift 한다. (1001 -> 10010)
4. multiplier register를 1 bit 오른쪽으로 shift 한다. (1001 -> 100)
5. 32bit 체제의 경우 위 과정 32번 반복한다. (10010 * 100)

 

위 곱셈기를 최적화한 곱셈기는 아래와 같다.

차이점은 product register에 값을 저장할 때, 상위 비트부터 채운다는 점이다.

1001 * 1011 의 연산을 예로 들어보자.

1. multiplier의 가장 낮은 bit가 1인 경우,
   product register에 있던 값과 multiplicand의 값을 더하고 그 값을 product register에 저장한다.
2. multiplier의 가장 낮은 bit가 0인 경우,
   product register의 값을 더하지 않고 그냥 내린다.
3. product register를 1 bit 오른쪽으로 shift 한다. (1001 -> 01001)
4. multiplier register를 1 bit 오른쪽으로 shift 한다. (1011 -> 101)
5. 반복

 

고속 곱셈기도 있다.

기존 곱셈기는 ALU 1개로 32스탭의 연산을 수행해야 했다.

고속 곱셈기는 ALU의 갯수가 31개나 필요하지만, 오직 5스탭의 연산만 수행하면 된다.

 

앞선 포스트에선 mul 명령어만 제시했었는데, mul 명령어는 연산 결과가 32 bits 보다 작은 경우에만 사용하는 것이 좋다.

이보다 큰 경우에는 다음과 같은 명령어들을 사용해야 한다.

명령어	읽기	기능
mult A, B	multiplication	A * B의 값 중 상위 32 bits를 HI에, 하위 32 bits를 LO에 저장
multu A, B	multiplication unsigned	A * B의 값 중 상위 32 bits를 HI에, 하위 32 bits를 LO에 저장. A, B: unsigned
mfhi A	move from HI	HI register의 값을 A로 가져온다.
mflo A	move from LO	LO register의 값을 A로 가져온다.

참고로 mul에서 연산 결과가 32 bits보다 큰 경우에는 하위 32 bits의 값이 저장된다.

 

 

Division (H/W)

하드웨어 레벨에서의 나눗셈을 하는 방식은 위 그림과 같다.

1001010 / 1000 의 연산을 예로 들어보자.

1. Divisor(1000)은 뒤에 32 bits를 0으로 채워 64 bit 취급하고,     Remainder은 그대로 32 bits 취급한다. 2. Remainder의 초기값은 Dividend(1001010)로 설정한다.  3. Remainder - Divisor가 음수인 경우     Remainder + Divisor를 통해 원래 값을 복구시키고,     Quotient를 1 bit 왼쪽으로 shift하고 그 값을 0으로 한다. 4. Remainder - Divisor가 양수인 경우     Quotient를 1 bit 왼쪽으로 shift하고 그 값을 1으로 한다. 5. Divisor register를 1 bit 오른쪽으로 shift한다. 6. 33번 반복 (초기 Quotient가 null에서 시작하기 때문)

나눗셈기 역시 최적화과 고속 버전이 있지만 생략한다.

 

나눗셈의 경우 아래의 명령어를 지원한다.

명령어	읽기	기능
div A, B	division	A / B의 값 중 나머지를 HI에, 몫을 LO에 저장
divu A, B	division unsigned	A / B의 값 중 나머지를 HI에, 몫을 LO에 저장. A, B: unsigned
mfhi A	move from HI	HI register의 값을 A로 가져온다.
mflo A	move from LO	LO register의 값을 A로 가져온다.

 

 

Floating Point (FP)

IEEE Std. 754-1985 표준에 따라 Scientific notaion를 normalize한 값을 저장한다.

32, 64 bits를 사용하는 지에 따라 Signle, Double precision으로 나뉘어 사용한다.

bit로는 위와 같이 역할이 나뉘어 저장되며, 이를 다음과 같이 해석할 수 있다.

$$ x = (-1)^{S} \times (1 + Fraction) \times 2^{Exponent - Bias} $$

 

Single precision의 경우 Exponent가 나타낼 수 있는 값은 2^8 = 256이므로

Bias는 127로 설정하여 이론상 2^-127 ~ 2^128 까지의 수를 표현할 수 있고,

Double precision의 경우 Exponent가 나타낼 수 있는 값은 2^11 = 2048이므로

Bias는 1023으로 설정하여 이론상 2^-1023 ~ 2^1024 까지의 수를 표현할 수 있다.

 

다만, Exponent의 값 중 00..00, 11..11은 예약되어 있어 사용할 수 없다.

따라서 실제 표현 가능한 수는 위 이론치보다 작아진다.

Fraction = 00..00 인 경우 유효 숫자는 1.0이 되고,
따라서 표현 가능한 가장 작은 값(절댓값 기준)은 다음과 같다.
$$ \pm 1.0 \times 2^{-126} \approx \pm 1.2 \times 10^{-38} $$

반대로 Fraction = 11.11인 경우 유효 숫자는 2.0에 거의 근접하게 되고,
따라서 표현 가능한 가장 큰 값(절댓값 기준)은 다음과 같다.
$$ \pm 2.0 \times 2^{127} \approx \pm 3.4 \times 10^{38} $$

Double precision의 경우에도 비슷하게 계산하면 다음과 같다.
$$ \pm 1.0 \times 2^{-1022} \approx \pm 2.2 \times 10^{308} $$
$$ \pm 2.0 \times 2^{1023} \approx \pm 1.8 \times 10^{308} $$

 

Fraction 파트는 각각 2^23, 2^52의 정확도를 갖고 있는데 log 함수를 씌워보면

각각 대략 6, 16의 값이 나온다. 즉 10진수에선 소숫점 아래 6, 16 만큼의 정확도를 갖는 것이다.

 

FP을 10 -> 2진수로 변환하는 과정은 다음과 같다.

일단 2의 지수승 꼴로 표현되는 과정에서 normalize한 형식으로 변환해야 한다.

간단히 말하면 2를 곱하거나 나누어서 소수점보다 왼쪽에 있는 값이 1로 변할 때 까지 하면 된다.

이후, 소수점 오른쪽 부분을 2진수로 분해한다.

그리고 위 공식에 맞게 S, Expo, Frac 파트를 구하면 된다.

 

 

FP Adder (H/W)

FP Adder는 아주 복잡해서 한 연산이 1 clock cycle에 끝나기 어려운 연산이다.

그래서 pipeline 기법을 통해 여러 사이클에 연산이 처리되도록 구현되어 있다.

(그러니까 코딩할 때 가급적이면 FP연산은 지양하는게 성능 향상에 도움이 된다)

스탭별로 살펴보자. (위 경우는 A의 Exponent가 더 큰 경우라고 가정한다)

- Step 1

1. Exponent 파트를 Small ALU에서 A-B를 계산한다.
2. Control에서 위 값이 양수(A가 더 큼)면 그 차이만큼 B의 Fraction을 오른쪽으로 shift하고,
   양수(B가 더 큼)면 그 차이만큼 A의 Fraction을 오른쪽으로 shift한다.
3. 그렇게 Exponent 단위가 맞춰진 A, B의 Fraction는 Big ALU로 들어가게 된다.
4. 왼쪽에서는 큰 쪽의 Exponent값이 Incre/Decrement로 들어가게 된다.

 

- Step 2

1. Big ALU에서 덧셈 연산이 수행된다.

 

- Step 3

1. 연산 결과에 따라 normalize한다.
   이 때 Fraction, Exponent 값이 shift된다.

 

- Step 4

1. 유효 숫자에 맞게 Round 된다.
2. Round 했을 때 normalize 상태가 깨지면 Step 3으로 되돌아간다.

 

요약하자면 다음과 같다.

1. Decimal point (Exponent)를 Align 한다. 이 때, 작은 값을 shift해서 큰 값에 맞춘다.
2. Significant (Fraction)을 더한다.
3. normaize하고 over/underflow를 체크한다.
4. 필요에 따라 round 하고 renormalize한다.

 

 

FP Instructions

FP를 위한 별도의 레지스터와 연산자를 가지고 있다.

형 변환이 필요한 경우에는 메모리에 sw, lw 하는 방식으로 형변환 할 수 있다.

 

- Register

레지스터	사용처
$f0 ~ $f31	FP 전용 레지스터. Double precision의 경우에는 $f0/$f1, $f2/$f3 이렇게 둘 씩 묶어쓴다. (명령어에선 앞에 레지스터 하나만 씀)

 

- Instructions

* 생략이 많음, 이전 포스트와 비교하면서 보면 좋음.

MIPS Instruction set

명령어	기능
lwc1, swc1, ldc1, sdc1 A, c(B)  l.s, s.s, l.d, s.d A, c(B)	A에 B + c offset의 데이터를 load, save. Single, Double precision
add.s, sub.s, mul.s, div.s A, B, C	B ? C 사칙연산의 결과를 A에 저장. Single precision
add.d, sub.d, mul.d, div.d A, B, C	B ? C 사칙연산의 결과를 A에 저장. Double precision
c.xx.s, c.xx.d A, B (xx = eq, lt, le)	A와 B를 비교하고 true면 FP condition-code를 1, false면 0으로 설정
bc1t, bc1f L	FP condition-code가 true(1), false(0)이면 L로 jump

 

 

- Example: F to C 

float f2c (float fahr) {
    return ((5.0 / 9.0) * (fahr - 32.0));
}

fahr = f12, result in f0
literal in global memory space(gp)

f2c: lwc1 $f16, const5($gp)  // FP의 경우 immediate load가 불가능하다.
        lwc1 $f18, const9($gp)  // 따라서 gp에서 offset 계산을 통해 load 한다.
        div.s $f16, $f16, $f18
        lwc1 $f18, const32($gp)
        sub.s $f18, $f12, $f18
        mul.s $f0, $f16, $f18
        jr $ra

 

- Example: Array multiplication

void mm (double x[][], double y[][], double z[][]) {
    int i, j, k;
    for (i = 0; i != 32; i += 1)
        for (j = 0; j != 32; j += 1)
            for (k = 0; k != 32; k += 1)
                // x[i][j] == x[i*32 + j]
                x[i][j] = x[i][j] + y[i][k] * z[k][j];
}

x = a0, y = a1, z = a2
i = s0, j = s1, k = s2

        addi $t0, $zero, 32  // 자주 쓰는 상수를 레지스터에 저장하면 편함
        addi $s0, $zero, $zero
L1:   addi $s1, $zero, $zero
L2:  addi $s2, $zero, $zero
        sll $t1, $s0, 5  // i*32
        addu $t1, $t1, $s1  // i*32 + j
        sll $t1, $t1, 3  // double(8 bytes)라서 *8 addressing
        addu $t1, $a0, $t1
        l.d $f4, 0($t1)  // f4 = x[i][j]
L3:  sll $t2, $s0, 5
        addu $t2, $t2, $s2
        sll $t2, $t2, 3
        addu $t2, $a1, $t2
        l.d $f6, 0($t1)  // f6 = y[i][k]
        sll $t2, $s2, 5
        addu $t2, $t2, $s1
        sll $t2, $t2, 3
        addu $t2, $a2, $t2
        l.d $f8, 0($t1)  // f8 = z[k][j]
        mul.d $f6, $f6, $f8
        add.d $f4, $f4, $f4
        addiu $s2, $s2, 1
        bne $s2, $t0, L3
        s.d $f4, 0($t1)
        addiu $s1, $s1, 1
        bne $s1, $t0, L2
        addiu $s0, $s0, 1
        bne $s0, $t0, L1

 

 

SIMD (Single Instruction Multiple Data)

영상과 같이 병렬처리 해야하는 작업을 수행할 때 연산 속도를 비약적으로 향상시킬 수 있는 기술.

예로 들어 128-bit adder는 아래와 같이 사용할 수 있다.

• 8-bit adds * 16
• 16-bit adds * 8
• 32-bit adds * 4

 

- SSE2 (Streaming SIMD Extension 2)

4개의 128-bit register를 추가해 아래와 같은 FP 연산을 가능케 하는 기술

• 64-bit Double precision * 2
• 32-bit Double precision * 4

 

아래와 같은 방법으로 행렬 곱을 최적화 할 수 있다.

// C = C + A * B
// Unoptimized
void dgemm (int n, double *A, double *B, double *C) {
    for (int i=0; i<n; ++i)
        for (int j=0; i<n; ++j) {
            double cij = c[i+j*n];
            for (int k=0; k<n; k++)
                cij += A[i+k*n] * B[k+j*n];
            c[i+j*n] = cij;
        }
}

// Optimized
#include <x86intrin.h>

void dgemm (int n, double *A, double *B, double *C) {
    for (int i=0; i<n; i+=8)  // 대략 8배 빨라짐
        for (int j=0; j<n; ++j) {
            __m512d c0 = _mm512_load_pd(C + i + j*n);
            for (int k=0; k<n; k++) {
                __m512d bb = _mm512_broadcastsd_pd(__mm_load_sd(B + j*n + k));
                c0 = _mm512_fmadd_pd(_mm512_load_pd(A + n*k + i), bb, c0);
            }
            _mm512_store_pd(C + i + j*n, c0);
        }
}

_로 시작하는 함수는 SSE2 instruction과 1-1로 매핑되는 함수들이다.

따라서 반복문의 범위가 짧아지고, assembly code 자체의 길이도 짧아질 수 있어

시간이 매우 크게 절약될 수 있다.

 

 

연산 주의사항

- Right shift (Division)

unsigned integer인 경우에 right로 n bit shift하면 2^n으로 나누는 효과가 있다.

signed integer인 경우에는 sign-bit를 replicate 하는 방법으로 extension해야 논리적인 오류가 없다.

 

단, 이렇게 Division 하는 경우에는 -∞로 round 하는 효과가 발생한다.

즉, 버림하게 된다.

 

- Associativity

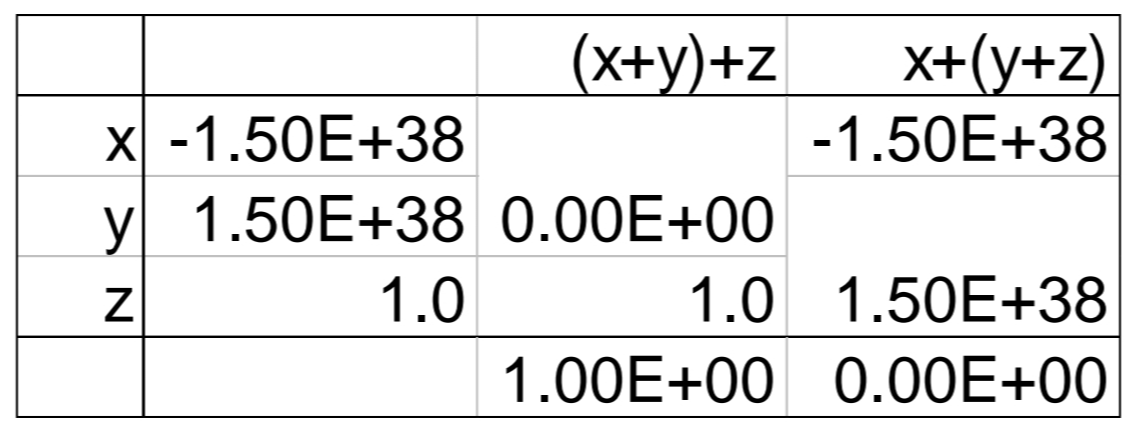
위와 같이 큰 값을 연산하는 경우 연산 순서에 따라 결과가 달라질 수 있다.

그 이유는 Exponent에 따라 Fraction 파트가 shift 되는데,

이 때 유효 숫자보다 작은 값은 그 값이 무시되기 때문에 연산 결과가 달라질 수 있다.

 

따라서 이런 값을 연산하는 경우에는 검증하는 단계가 필요하다.